L Shapes from Two Pentominoes
A pentomino is a figure made of five squares joined
edge to edge.
There are 12 such figures, not distinguishing reflections and rotations.
They were first enumerated and studied by Solomon Golomb.
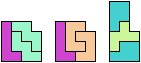
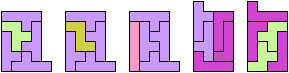
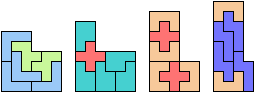
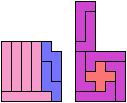
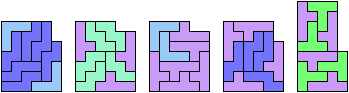
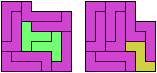
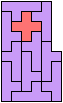
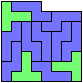
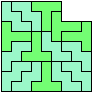
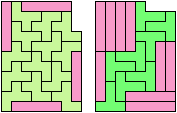
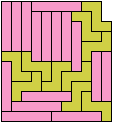
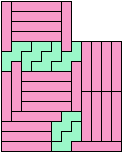
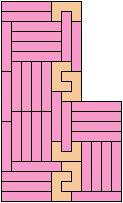
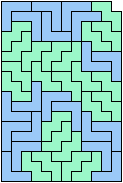
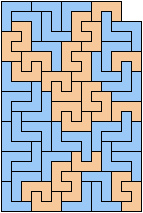
Here I study
the problem of forming an L-shaped (six-sided) polyomino
with copies of two pentominoes, using at least one of each.
If you find a smaller solution than one of mine,
please write!
See also
L Shapes from Three Pentominoes
and
L Shapes from Pentacube Pairs.
I use Solomon W. Golomb's original names for the pentominoes:
This table shows the smallest total number of two pentominoes known to be
able to tile an L-shaped polyomino:
| F | I | L | N | P | T | U | V | W | X | Y | Z |
|---|
| F
| *
| 17
| 5
| ×
| 3
| ×
| 2
| 6
| ×
| ×
| 5
| ×
|
|---|
| I
| 17
| *
| 2
| 7
| 2
| 17
| 40
| 2
| 32
| ×
| 5
| 26
|
|---|
| L
| 5
| 2
| *
| 2
| 2
| 9
| 3
| 2
| 3
| 7
| 5
| 9
|
|---|
| N
| ×
| 7
| 2
| *
| 2
| 12
| 6
| 8
| ×
| ×
| 8
| ×
|
|---|
| P
| 3
| 2
| 2
| 2
| *
| 2
| 2
| 2
| 4
| 6
| 2
| 2
|
|---|
| T
| ×
| 17
| 9
| 12
| 2
| *
| 46
| ×
| 15
| ×
| 8
| ×
|
|---|
| U
| 2
| 40
| 3
| 6
| 2
| 46
| *
| 58
| ×
| 6
| 2
| ×
|
|---|
| V
| 6
| 2
| 2
| 8
| 2
| ×
| 58
| *
| 43
| ×
| 8
| 2
|
|---|
| W
| ×
| 32
| 3
| ×
| 4
| 15
| ×
| 43
| *
| ×
| 8
| ×
|
|---|
| X
| ×
| ×
| 7
| ×
| 6
| ×
| 6
| ×
| ×
| *
| 11
| ×
|
|---|
| Y
| 5
| 5
| 5
| 8
| 2
| 8
| 2
| 8
| 8
| 11
| *
| 5
|
|---|
| Z
| ×
| 26
| 9
| ×
| 2
| ×
| ×
| 2
| ×
| ×
| 5
| *
|
|---|
So far as I know, these solutions
have the fewest possible tiles.
They are not necessarily uniquely minimal.
2 Tiles
3 Tiles
4 Tiles
5 Tiles
6 Tiles
7 Tiles
8 Tiles
9 Tiles
11 Tiles
12 Tiles
15 Tiles
17 Tiles
26 Tiles
32 Tiles
40 Tiles
43 Tiles
46 Tiles
58 Tiles
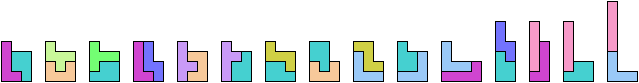
Last revised 2021-03-20.
Back to Polyomino and Polyking Tiling
<
Polyform Tiling
<
Polyform Curiosities
Col. George Sicherman
[ HOME
| MAIL
]