Three-Pentomino Rectangles

  • Introduction
  • Nomenclature
  • Table
  • Solutions

    • Introduction

    A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

    The problem of arranging copies of a polyomino to form a rectangle has been studied for a long time. The problem of arranging copies of two polyominoes to form a rectangle was studied by Earl Kramer and Frits Göbel in Tiling Rectangles with Pairs of Pentominoes, Journal of Recreational Mathematics 16(3) (1983), 198–206. Later it was studied in Rodolfo Kurchan's Puzzle Fun, Issue 19, Tyling with Pairs of Polyominoes. Still later, the problem was studied further in Erich Friedman's Math Magic for August 2010.

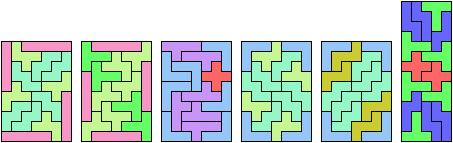
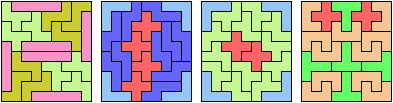
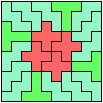
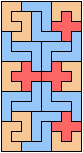
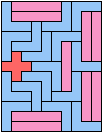
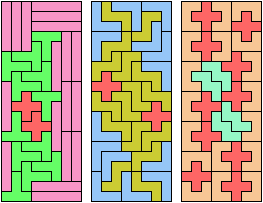
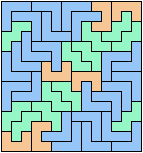
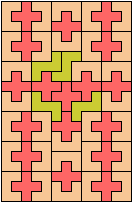
    Here I study the problem of arranging copies of three pentominoes to form a rectangle, using at least one of each.

    Carl Schwenke and Johann Schwenke improved on one of my solutions.

    See also Three-Pentomino Balanced Rectangles.

    Nomenclature

    I use Solomon W. Golomb's original names for the pentominoes:

    Table of Results

    This table shows the smallest total number of pentominoes known to be able to tile a rectangle with copies of three given pentominoes, using at least one of each.

    FIL 4FNV 6FUZ 5INU 5IUY 3LPV 3LWZ 6NVW 8PVX 6TXZ —
    FIN 11FNW —FVW 10INV 4IUZ 7LPW 4LXY 6NVX 14PVY 3TYZ 6
    FIP 4FNX —FVX 15INW 9IVW 7LPX 6LXZ 8NVY 5PVZ 3UVW 30
    FIT 10FNY 5FVY 5INX 19IVX 24LPY 3LYZ 5NVZ 3PWX 6UVX 4
    FIU 3FNZ —FVZ 5INY 5IVY 4LPZ 3NPT 3NWX —PWY 3UVY 3
    FIV 5FPT 4FWX —INZ 7IVZ 3LTU 5NPU 3NWY 7PWZ 4UVZ 5
    FIW 11FPU 3FWY 6IPT 3IWX 20LTV 4NPV 3NWZ —PXY 5UWX 23
    FIX 15FPV 4FWZ —IPU 3IWY 5LTW 5NPW 5NXY 7PXZ 6UWY 4
    FIY 5FPW 5FXY 7IPV 3IWZ 7LTX 8NPX 6NXZ —PYZ 4UWZ —
    FIZ 15FPX 8FXZ —IPW 4IXY 6LTY 4NPY 3NYZ 6TUV 5UXY 5
    FLN 5FPY 4FYZ 5IPX 5IXZ 15LTZ 5NPZ 4PTU 4TUW 15UXZ 23
    FLP 3FPZ 4ILN 3IPY 3IYZ 6LUV 5NTU 4PTV 3TUX 17UYZ 5
    FLT 6FTU 5ILP 3IPZ 3LNP 3LUW 6NTV 5PTW 4TUY 5VWX 57
    FLU 3FTV 10ILT 3ITU 7LNT 4LUX 3NTW 11PTX 6TUZ 16VWY 5
    FLV 4FTW 14ILU 4ITV 6LNU 4LUY 3NTX 11PTY 3TVW 5VWZ 8
    FLW 5FTX —ILV 3ITW 7LNV 4LUZ 5NTY 5PTZ 5TVX —VXY 8
    FLX 8FTY 6ILW 4ITX 17LNW 6LVW 5NTZ 11PUV 4TVY 5VXZ 21
    FLY 5FTZ —ILX 6ITY 5LNX 6LVX 8NUV 6PUW 5TVZ 6VYZ 4
    FLZ 4FUV 3ILY 3ITZ 10LNY 4LVY 4NUW 7PUX 3TWX 20WXY 9
    FNP 4FUW 4ILZ 5IUV 7LNZ 5LVZ 3NUX 7PUY 3TWY 7WXZ —
    FNT 10FUX 5INP 3IUW 11LPT 3LWX 9NUY 4PUZ 4TWZ 14WYZ 6
    FNU 4FUY 3INT 6IUX 4LPU 3LWY 5NUZ 8PVW 4TXY 9XYZ 7

    Solutions

    So far as I know, these solutions have minimal area. They are not necessarily uniquely minimal.

    3 Tiles

    4 Tiles

    5 Tiles

    6 Tiles

    7 Tiles

    8 Tiles

    9 Tiles

    10 Tiles

    11 Tiles

    12 Tiles

    13 Tiles

    14 Tiles

    16 Tiles

    18 Tiles

    20 Tiles

    21 Tiles

    24 Tiles

    26 Tiles

    32 Tiles

    42 Tiles

    52 Tiles

    57 Tiles

    Last revised 2024-02-28.

    Back to Polyomino and Polyking Tiling < Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]