Scaled Two-Pentomino Balanced Rectangles

  • Introduction
  • Nomenclature
  • Table
  • Solutions

    • Introduction

    A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

    It has long been known that only four pentominoes can tile rectangles:

    For other rectangles that these pentominoes tile, see Mike Reid's Rectifiable Polyomino Page.

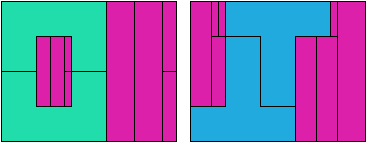
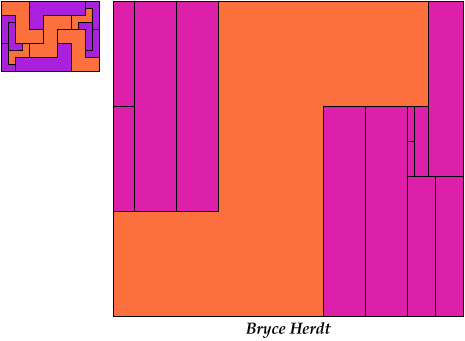
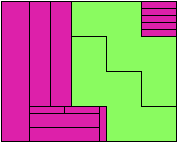
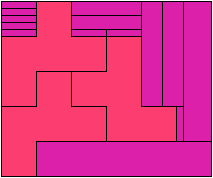
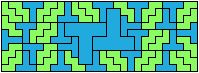
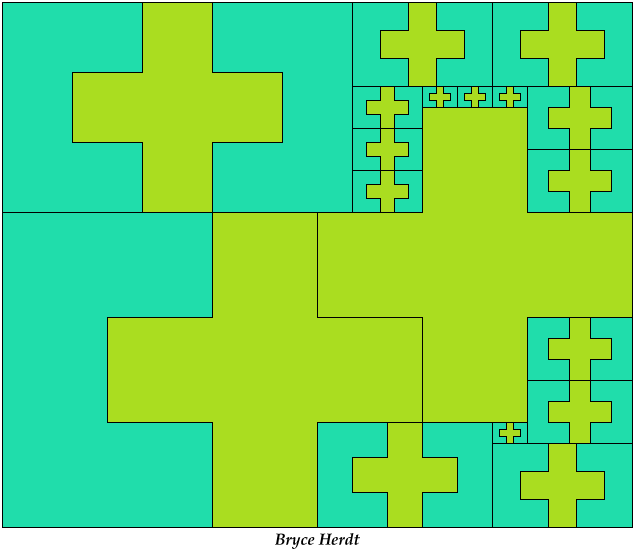
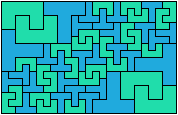
    On Balanced Two-Pentomino Rectangles I study the problem of tiling some rectangle with two pentominoes, using the same areas of each. Here I study the same problem, using the pentominoes in various sizes. If you find a better solution than one of mine, or solve an unsolved case, please write!

    Bryce Herdt sent some improved solutions.

    Nomenclature

    I use Solomon W. Golomb's original names for the pentominoes:

    Table

    This table shows the smallest total number of scaled pentominoes known to be able to tile a rectangle in equal areas.

    FILNPTUVWXYZ
    F * 17 4 × 8 × 12 4 × × 8 ×
    I 17 * 4 11 4 10 10 9 15 23 8 13
    L 4 4 * 4 4 8 4 4 4 31 8 13
    N × 11 4 * 4 24 4 4 × × 8 ×
    P 8 4 4 4 * 9 4 6 8 26 4 9
    T × 10 8 24 9 * 56 7 50 × 4 ×
    U 12 10 4 4 4 56 * 30 × 51 12 ×
    V 4 9 4 4 6 7 30 * 72 × 9 4
    W × 15 4 × 8 50 × 72 * × 14 ×
    X × 23 31 × 26 × 51 × × * 20 ×
    Y 8 8 8 8 4 4 12 9 14 20 * 8
    Z × 13 13 × 9 × × 4 × × 8 *

    Solutions

    So far as I know, these solutions have minimal tiles. They are not necessarily uniquely minimal.

    4 Tiles

    6 Tiles

    7 Tiles

    8 Tiles

    9 Tiles

    10 Tiles

    11 Tiles

    12 Tiles

    13 Tiles

    14 Tiles

    15 Tiles

    17 Tiles

    20 Tiles

    23 Tiles

    24 Tiles

    26 Tiles

    30 Tiles

    31 Tiles

    50 Tiles

    51 Tiles

    56 Tiles

    72 Tiles

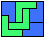
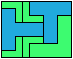
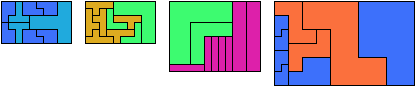
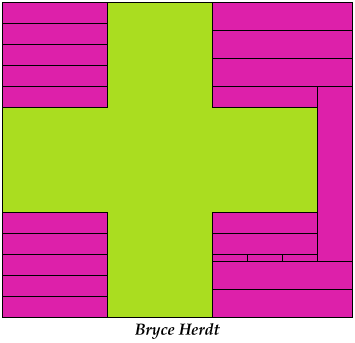
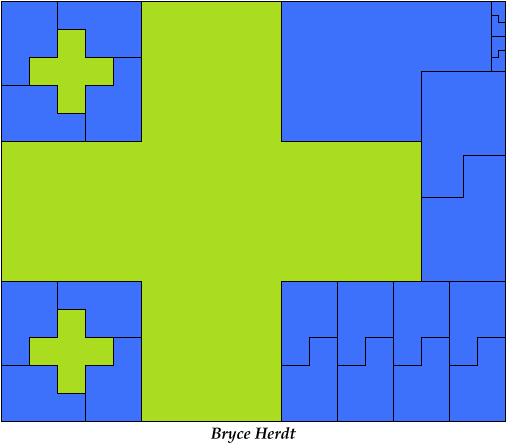
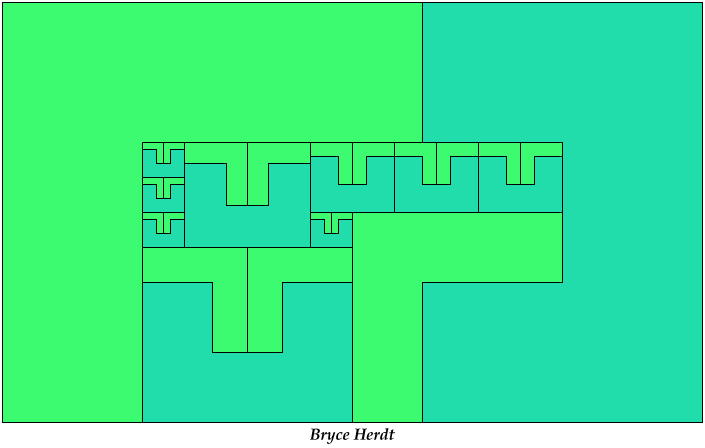
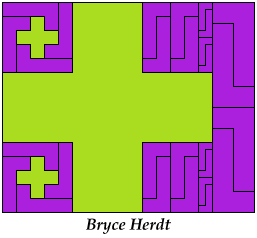
    Last revised 2021-05-19.

    Back to Polyform Tiling < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]