Scaled Two-Pentomino Rectangles

Introduction

A pentomino is a figure made of five squares joined edge to edge. There are 12 such figures, not distinguishing reflections and rotations. They were first enumerated and studied by Solomon Golomb.

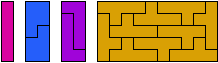
It has long been known that only four pentominoes can tile rectangles:

For other rectangles that these pentominoes tile, see Mike Reid's Rectifiable Polyomino Page.

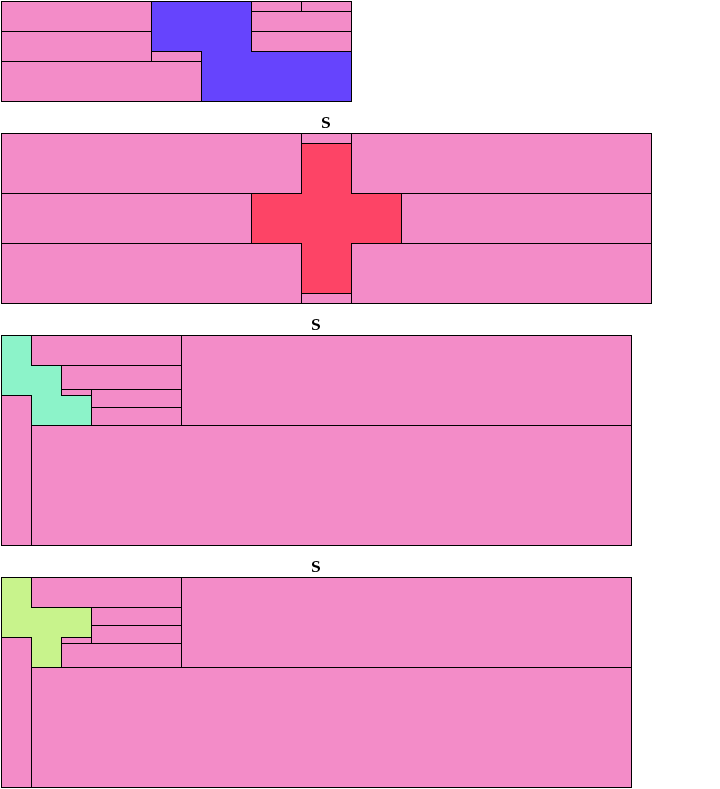
Here I show which pairs of pentominoes can tile a rectangle, using the pentominoes at various sizes. If you find a solution better than one of mine, please write!

Nomenclature

I use Solomon W. Golomb's original names for the pentominoes:

This table shows the fewest scaled pentominoes known to be able to tile a rectangle, using at least one of each pentomino. The rectangles are not necessarily the smallest that can be tiled, only the smallest that can be tiled with the fewest tiles.

	F	I	L	N	P	T	U	V	W	X	Y	Z
F	*	9	4	×	6	×	6	4	×	×	5	×
I	9	*	3	9	3	7	6	4	9	9	6	7
L	4	3	*	4	3	8	4	4	4	5	6	7
N	×	9	4	*	4	10	4	4	×	×	6	×
P	6	3	3	4	*	3	4	3	4	5	3	3
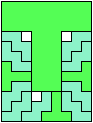
T	×	7	8	10	3	*	56	7	16	×	4	×
U	6	6	4	4	4	56	*	3	×	3	6	6
V	4	4	4	4	3	7	3	*	30	×	6	3
W	×	9	4	×	4	16	×	30	*	×	10	×
X	×	9	5	×	5	×	3	×	×	*	5	×
Y	5	6	6	6	3	4	6	6	10	5	*	5
Z	×	7	7	×	3	×	6	3	×	×	5	*

Solutions

So far as I know, these solutions have the fewest possible tiles. They are not necessarily uniquely minimal.

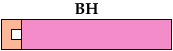
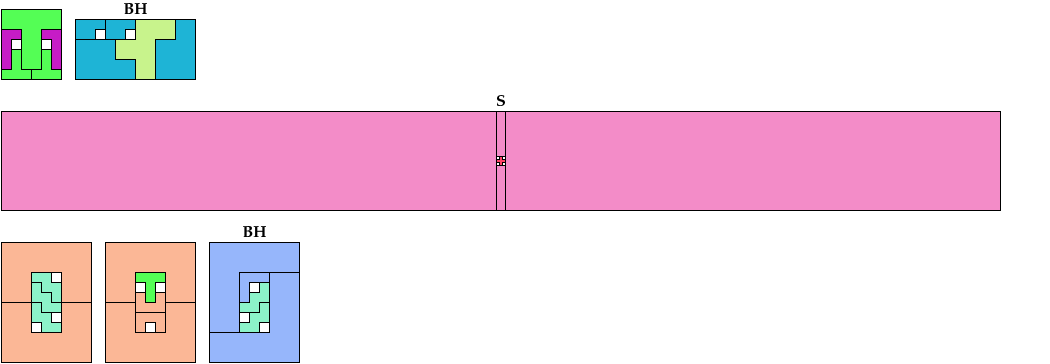
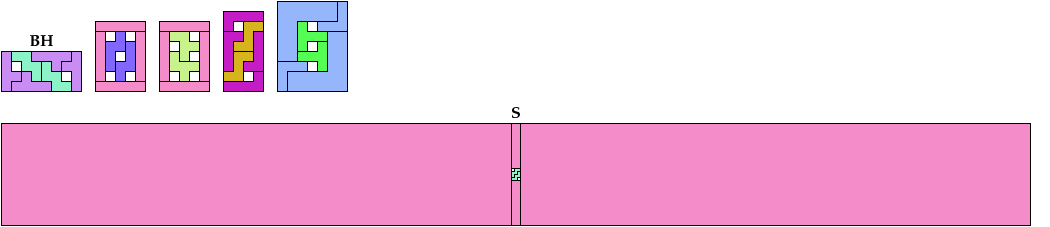
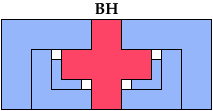
Solutions labeled BH are by Bryce Herdt. Solutions labeled S are by Carl Schwenke and Johann Schwenke.

3 Tiles

4 Tiles

5 Tiles

6 Tiles

7 Tiles

8 Tiles

9 Tiles

10 Tiles

16 Tiles

30 Tiles

56 Tiles

Variants with Holes

Jenard Cabilao suggested allowing one-cell holes in rectangles. The holes may not touch the perimeter or one another, not even at corners.

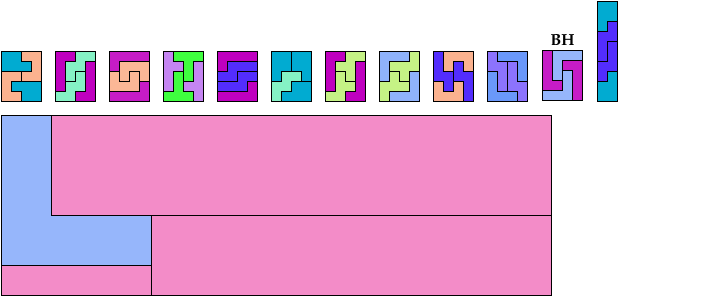
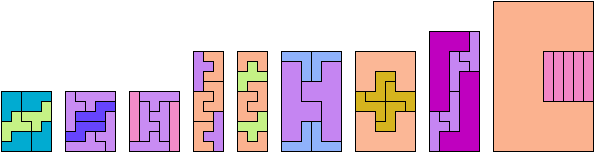
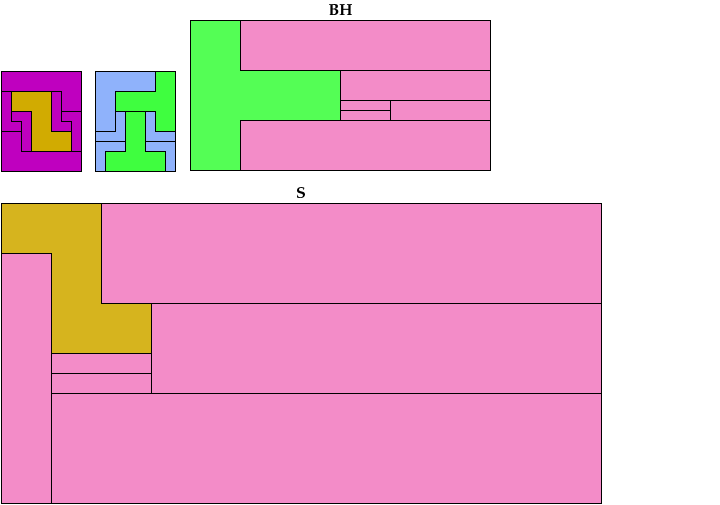
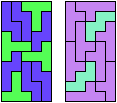
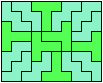
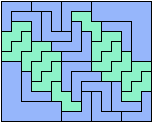
These are holey solutions with fewer tiles than the corresponding holeless solutions.