In general, it is easier to tile rectangles than L shapes, because rectangles can often be tiled with rotary symmetry. However, for some polyominoes the minimal rectangles cannot be tiled symmetrically.
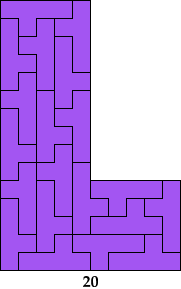
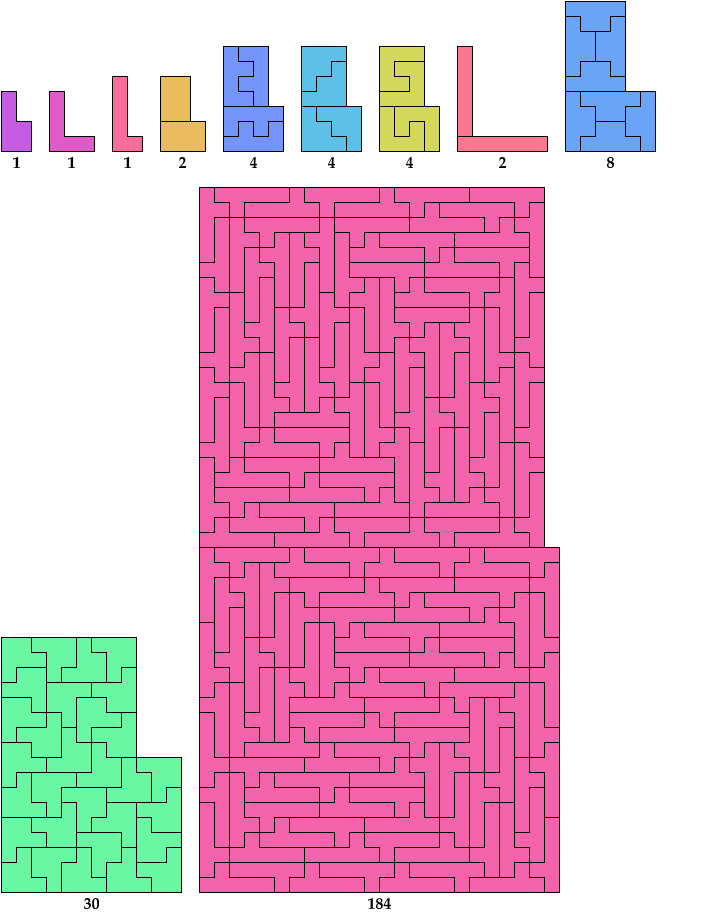
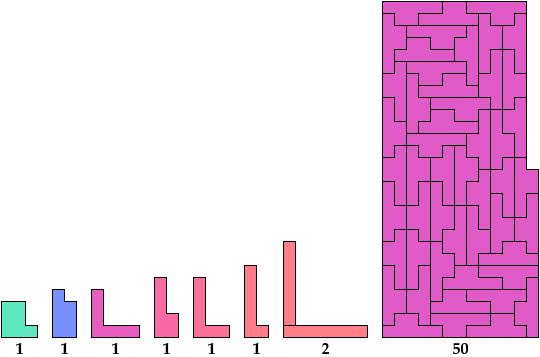
Here I show the smallest known L shapes, measured by area, that can be tiled with given polyominoes. If you find a smaller solution or solve an unsolved case, please write.
See also Tiling an L Shape with the 12 Pentominoes.
The largest octomino solution is formed by joining two rectangular tilings. It is not likely to be minimal.
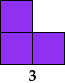

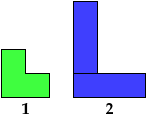
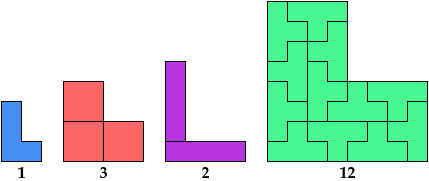
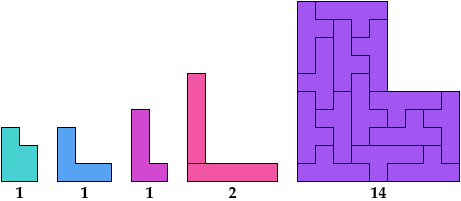
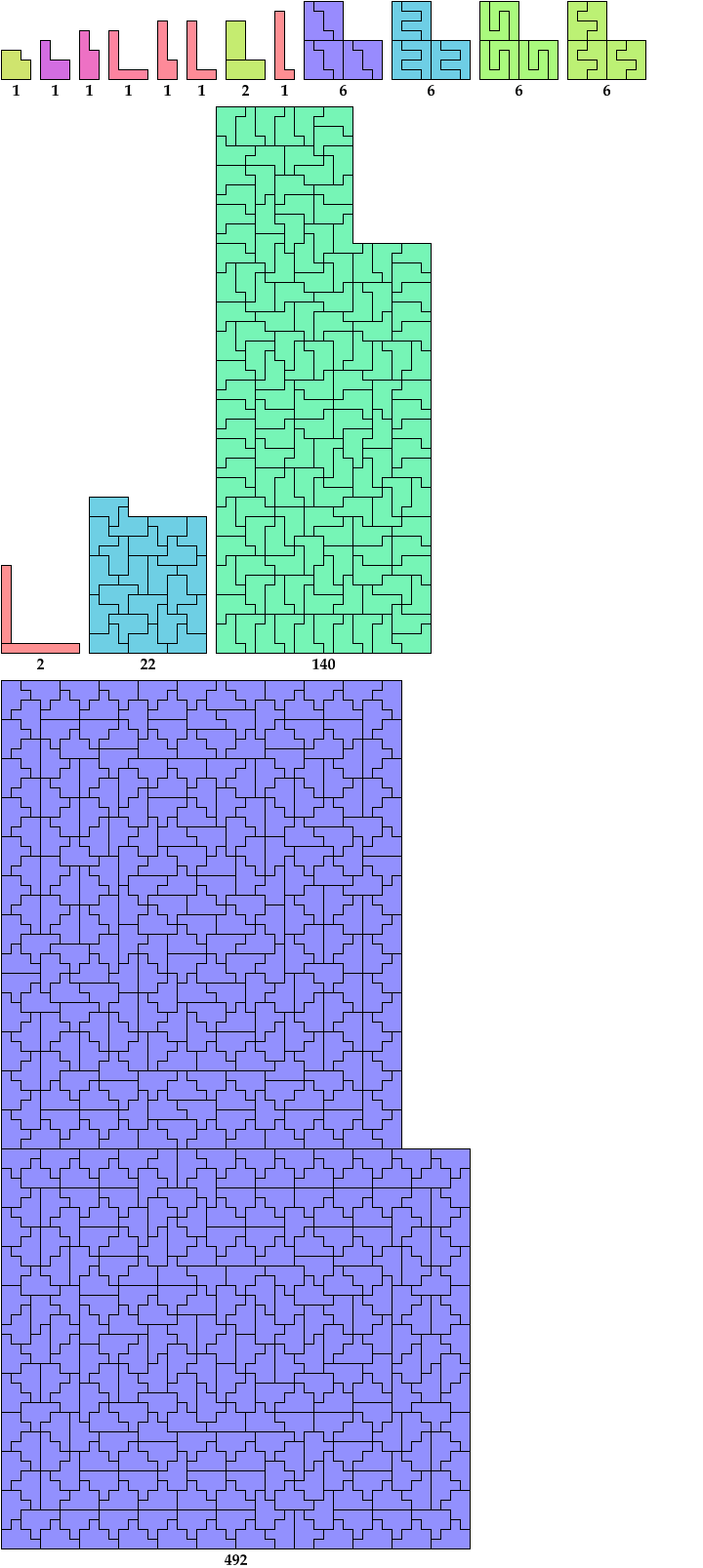
The largest hexomino, heptomino, and octomino solutions are formed by joining two rectangular tilings. They may not be the smallest possible solutions.

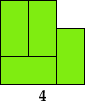
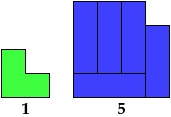
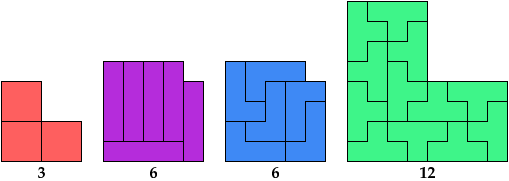
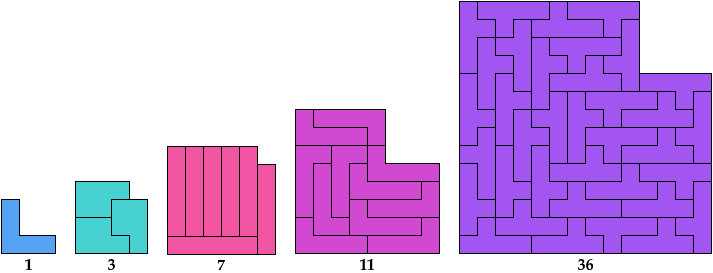

Last revised 2025-08-03.