Two-Pentomino Magic Squares

The May 2007 issue of Erich Friedman's Math Magic dealt with arranging copies of a polyomino in a square so that every row and column of the square contained the same number of occupied cells. Such arrangements are called Binary Incomplete Block diagrams, or BIB diagrams. They are not usually constructed with polyominoes!

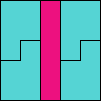
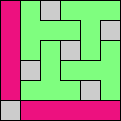
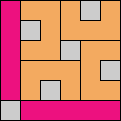
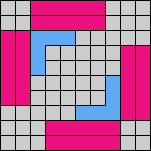
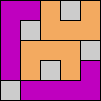
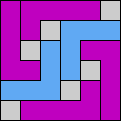
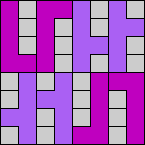
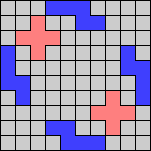
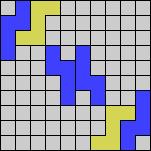
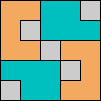
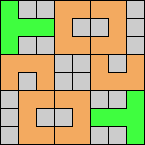
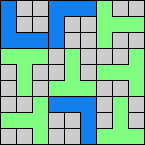
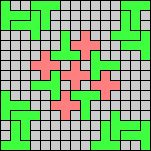
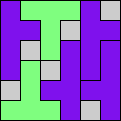
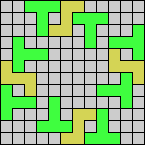
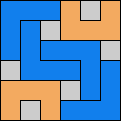
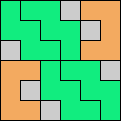
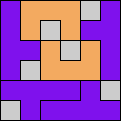
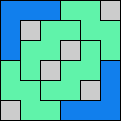
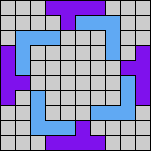
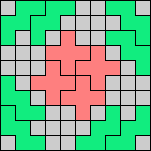
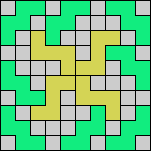
Issue 34 of Rodolfo Marcelo Kurchan's Puzzle Fun extended this work, showing minimal solutions for various numbers of cells and for single sets of the polyominoes of a given size.

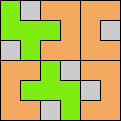
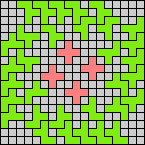
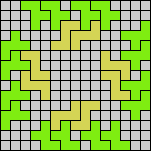
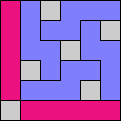
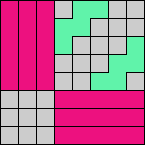
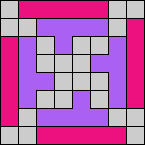
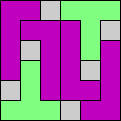
Here I show magic squares for pairs of pentominoes, using at least one copy of each. As in Math Magic, solutions have as few tiles as are known to be possible.

5F + 5I5F + 5L5F + 5N5F + 5P5F + 5T5F + 5U
5F + 5V5F + 5W5F + 5X5F + 5Y5F + 5Z5I + 5L
5I + 5N5I + 5P5I + 5T5I + 5U5I + 5V5I + 5W
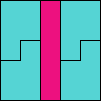5I + 5X5I + 5Y5I + 5Z5L + 5N5L + 5P5L + 5T
5L + 5U5L + 5V5L + 5W5L + 5X5L + 5Y5L + 5Z
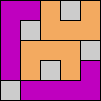5N + 5P5N + 5T5N + 5U5N + 5V5N + 5W5N + 5X
5N + 5Y5N + 5Z5P + 5T5P + 5U5P + 5V5P + 5W
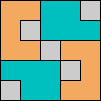5P + 5X5P + 5Y5P + 5Z5T + 5U5T + 5V5T + 5W
5T + 5X5T + 5Y5T + 5Z5U + 5V5U + 5W5U + 5X
5U + 5Y5U + 5Z5V + 5W5V + 5X5V + 5Y5V + 5Z
5W + 5X5W + 5Y5W + 5Z5X + 5Y5X + 5Z5Y + 5Z
none

Last revised 2021-09-09.

Back to Polyform Exclusion, Equalization, Variegation, and Integration < Polyform Curiosities
Col. George Sicherman [ HOME | MAIL ]