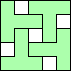
In the May 2007 issue of his web feature Math Magic, Erich Friedman defined a polyomino magic square as an arrangement of one or more copies of a given polyomino in a square grid, having the same number of cells occupied in every row and column of the square. Here is an example of Erich's:

It has 4 occupied cells in each row and column.
Some polyominoes can be shown to have no magic square. Others have no known magic square and no known proof that none exists.
Issue 34 of Rodolfo Marcelo Kurchan's magazine Puzzle Fun extended Erich's results to squares of arbitrary size.
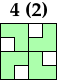
Some minimal polyomino magic squares do not have all their tiles connected at edges. Here is an example:

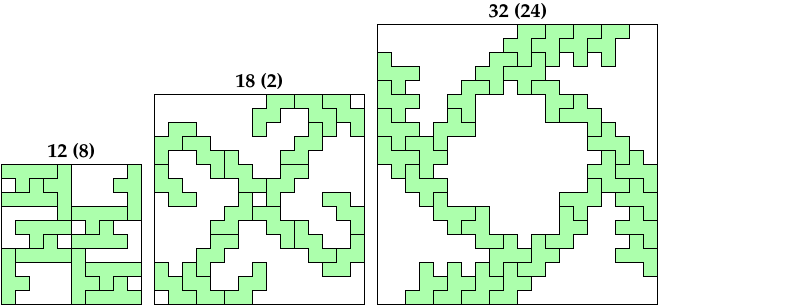
Here I show minimal connected magic squares for polyominoes whose minimal magic squares shown on Erich's page are not connected. The number in parentheses tells how many tiles are in the minimal disconnected solution.


Last revised 2022-08-01.