Zucca's Challenge Problem for Tetrahexes

Livio Zucca's Tetrominoes Challenge Page challenges you to find plane regions that can be tiled with each of a given set of tetrominoes and no others. Here I show solutions to the corresponding problem for tetrahexes. If you have a smaller solution for any of these sets, please let me know.

For extrominoes, see Zucca's Challenge Problem for Extrominoes. For polyiamonds, see Zucca's Challenge Problem for Polyiamonds.

Solutions

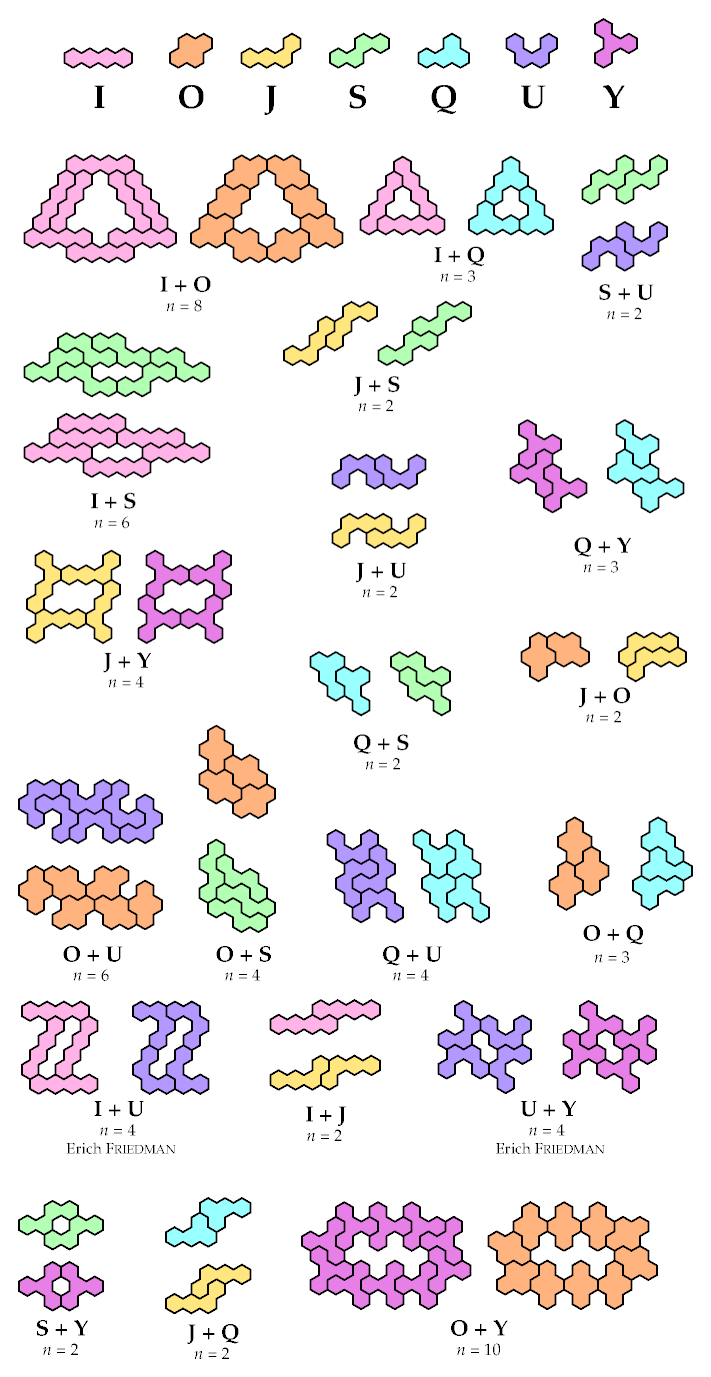
There are 7 tetrahexes, so a complete solution for Zucca's problem for tetrahexes has 120 cases! That's too many for me. Here are solutions for all the pairs but one. They may not be minimal. Thanks to Dr. Friedman for improving on some of my original results.

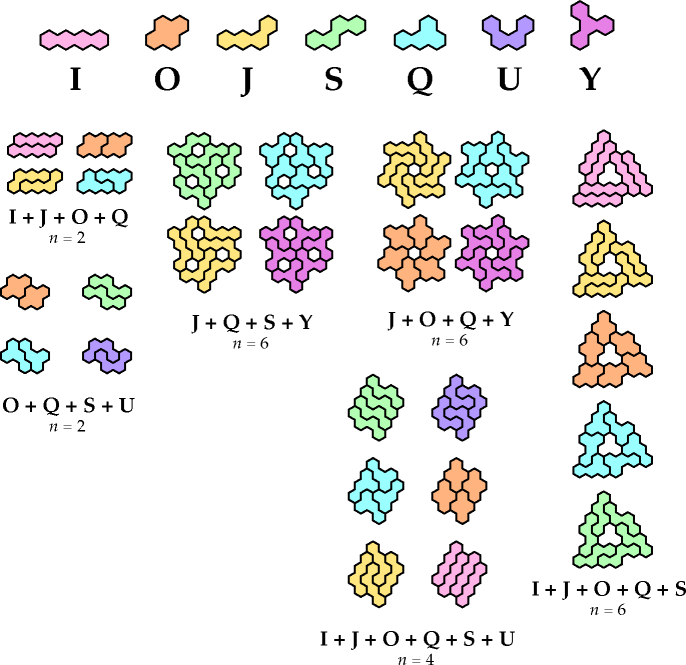
Pairs

Triplets

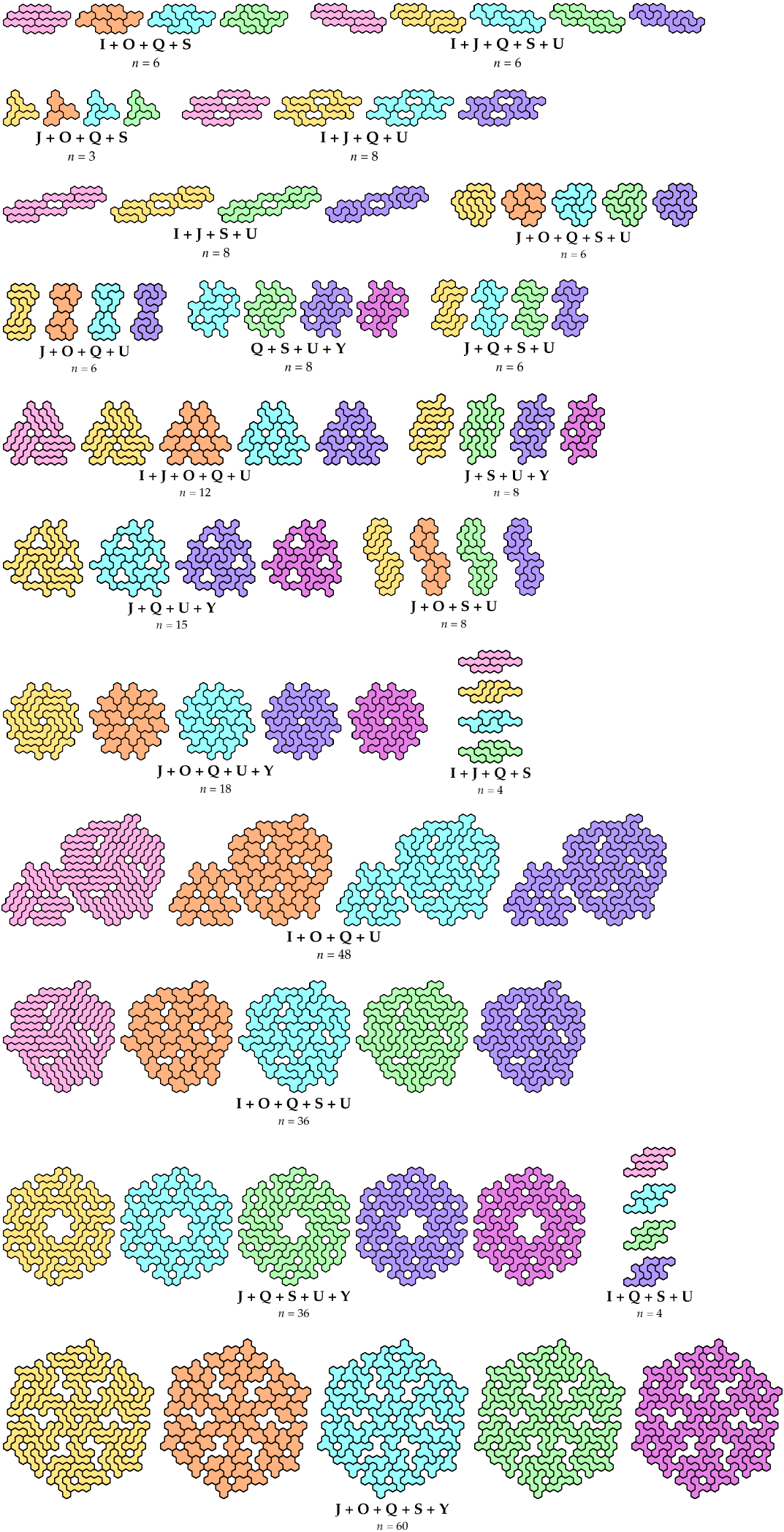
And here, by courtesy of Dr. Friedman or me or both, are some solutions for sets of three or more:

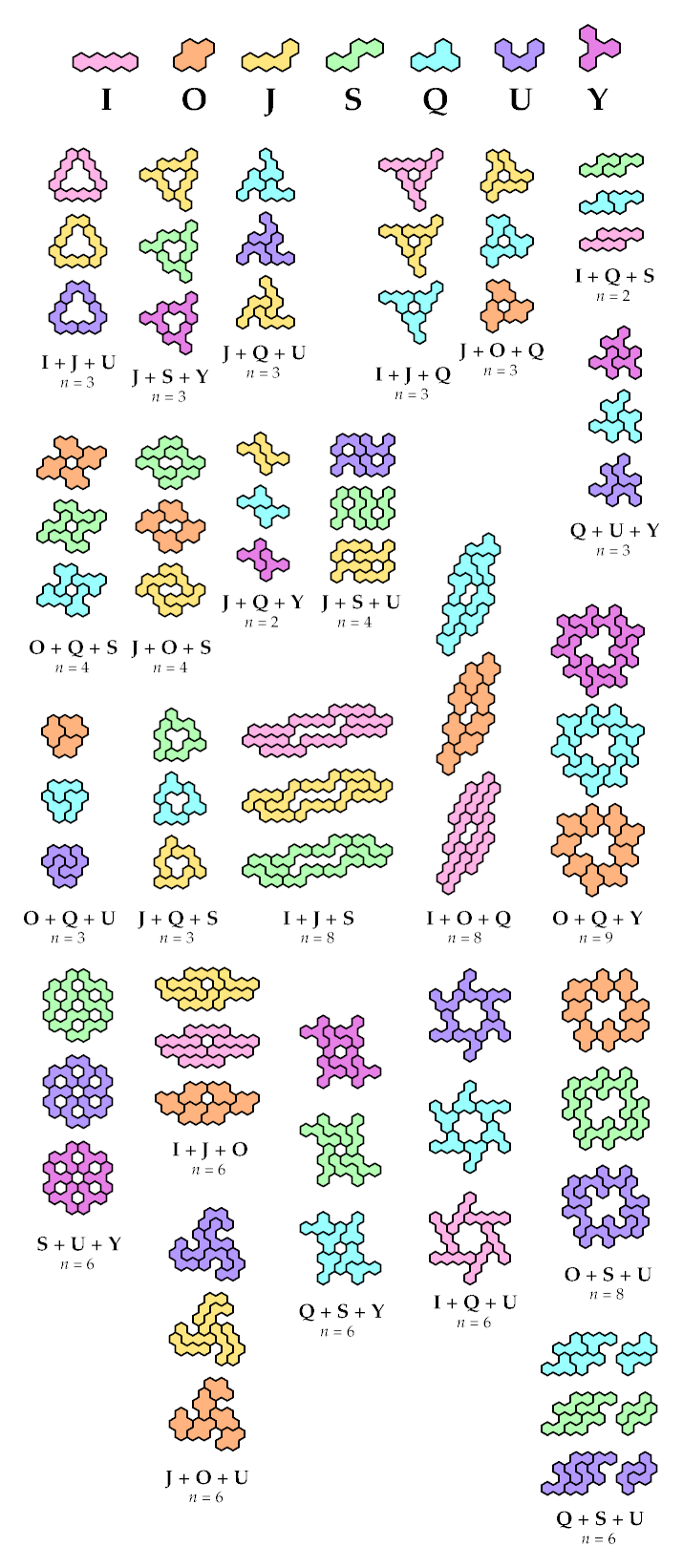
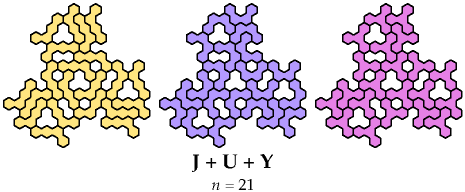
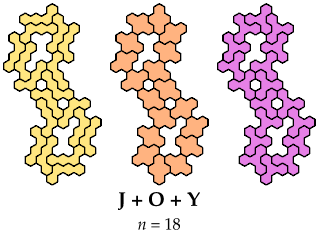
Bigger Sets

Last revised 2018-06-02.

Back to Multiple Compatibility < Polyform Compatibility < Polyform Curiosities

Col. George Sicherman [ HOME | MAIL ]