

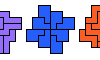
 | Holeless Triple Pentominoes. Holeless solutions for Livio Zucca's Triple Pentominoes. |
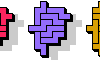 | Pentomino Odd Triples. Like Livio Zucca's Triple Pentominoes, with an odd number of tiles. |
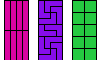 | Pento-Tetro-Tetrominoes. Given a pentomino and two tetrominoes, find a polyomino that each can tile. |
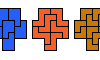 | Pento-Pento-Trominoes. Given two pentominoes and a tromino, find a polyomino that each can tile. |
 | Pento-Pento-Tetrominoes. Given two pentominoes and a tetromino, find a polyomino that each can tile. |
 | Quadruple Pentominoes. Given four different pentominoes, find a polyomino that each can tile. |
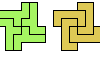 | Multiple Polyomino Compatibility. Figures that can be tiled by many polyominoes of the same order. |
 | Triple Hexiamonds. Given three hexiamonds, construct a figure that can be tiled with each. |
 | Hexi-Penti-Tetriamonds. Given a hexiamond, a pentiamond, and a tetriamond, construct a figure that can be tiled with each. |
 | Multiple Polyiamond Compatibility. Figures that can be tiled by many polyiamonds of the same order. |
 | Zucca's Challenge Problem for Polyiamonds. Given a set of polyiamonds of the same order, construct a figure that can be tiled with any member of the set and no other. |
 | Multiple Polyhex Compatibility. Figures that can be tiled by many polyhexes of the same order. |
 | Zucca's Challenge Problem for Tetrahexes. Given a set of tetrahexes, construct a figure that can be tiled with any member of the set and no other. |
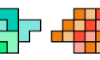 | Zucca's Challenge Problem for Extrominoes. Given a set of extrominoes, or extended trominoes, construct a figure that can be tiled with any member of the set and no other. |
 | Multiple Compatibility for Polypents. Figures that can be tiled by many polypents of the same order. |
 | Multiple Compatibility for Pentacubes. Figures that can be tiled by many polycubes of the same order. |