Detail of a French board marketed as
Solitaire Di Venezia,
solid ebony board with individually hand blown glass marbles.
|
These pages were created and are maintained by
George Bell
(gibell@comcast.net)
Last Modified January 23rd, 2016
Copyright © 2006–2016 by George I. Bell
2015 snapshot of this site
on recmath.org
|
|
We can merely mention bean-bags, peg-boards,
size and form boards, as some apparatus found useful
for the purpose of amusing and instructing the weak-minded.
Albutt's "System of Medicine", 1899, VIII, 246 [B3]
|
Table of Contents:
- Introduction
- Preliminaries
- Boards:
English,
6x6,
French,
Diamond41,
Diamond32,
Hoppers,
Wiegleb,
8x8,
9x9,
Rectangular,
Siege,
Generalized Cross,
Kralenspel
- General Boards:
Gridless,
Doughnut,
3D
- Online Games and Puzzles
- Solution Catalogs
- Computational Search Techniques
- How Hard Is Peg Solitaire?
- References
Introduction
Peg solitaire
is a classical puzzle commonly played on a 33-hole cross-shaped board
(also known as "the English board") or a
15-hole triangular board.
In England it is simply known as "Solitaire"; in the U.S. this is a
card game,
so it is identified as "Peg Solitaire".
Other people of a certain era know it as "Hi-Q" because a popular
version of the game sold under that trade name.
In India it is called "Brainvita".
This one-person game (or puzzle) first appeared in France in the late 17th century.
We know this because the puzzle is depicted in several art works of the period,
most notably the engraving by
Claude Auguste Berey
shown on the right.
The first mention of the game in print was in the French literary magazine
Mercure Galant in 1697.
Remarkably, this article escaped the notice of game historians for hundreds of years,
and it came to light only in 2014,
shortly after Mercure Galant
became available on the internet.
You can read more about this discovery in John Beasley's historical update
[P10].
|
The "Central Game"
|
|
A carefully
selected
sequence
of jumps
|
|
The starting
board position |
|
The target
board position |
|
|
The basic game consists of a cross-shaped board, often made of wood,
together with a set of pegs (or alternatively marbles).
To start the game, one fills the board with pegs except for the central hole.
A jump consists of jumping one peg over another into an empty spot in
the board, removing the peg jumped over from the board.
Diagonal jumps are not allowed (in the standard version of the game).
The goal is to choose a sequence of jumps and finish with as few pegs as
possible, ideally a single peg in the center.
It seems everyone (at least in my generation) has run into this puzzle at some point.
Boards range from drilled planks using golf tees,
to beautifully crafted hardwood boards with indentations for marbles,
including a nice rim around the edge for storage of marbles as they are removed.
Computer versions of the game are also common
(see my Javascript games below).
After unsuccessful attempts at a "manual solution", many people
(myself included) try to write a simple computer program to solve it.
Even if there are only 4-8 jumps available at each board position,
this can lead to a prohibitively large number of possible jump
sequences after only 15 jumps.
This game is much older than the computer, and it is remarkable how
much was proved about this game without the aid of computers.
Instead of trying to memorize a computer solution, or a
YouTube video,
the best way to remember a solution is to
understand "block removals" or "packages",
sequences of moves that remove a whole block of pegs but leave
the rest of the board untouched.
Once you understand and have mastered the "3-removal", "6-removal"
and "L-move", the central game rapidly goes from frustrating to
being quite simple
(for details, jump ahead to here,
or see [B1], [B3],
[W2] or [W20]).
After the central game above has been solved, what then?
We can try to find the "shortest" solution.
All solutions contain exactly 31 jumps,
because we start with 32 pegs and one is lost with each jump.
However, when the same peg jumps one or more pegs,
we call this one move.
The question is, what is the solution with the least number of moves?
This question may be rephrased more informally as: what is the solution
that involves touching the smallest number of pegs?
This question is more difficult than finding a
solution to the central game,
and we will return to it when discussing the English board.
The boards on this page have holes based on a square lattice; each hole
has (at most) 4 neighbors.
It is also possible to play on a triangular lattice,
where each hole has (at most) 6 neighbors.
I now have a separate page for
Triangular Peg Solitaire.
If you want some tips and solutions for the 15-hole triangular board,
check out my page on
tips and solutions for the Cracker Barrel Puzzle.
Below we will also discuss gridless boards.
James Dalgety [W13]
is a puzzle collector who owns many peg solitaire boards.
On his web page
he discusses design faults of peg solitaire boards,
which I include here for future puzzle designers.
Common design faults include:
- Not enough room for the fingers between the pegs or balls.
- No space, or not enough space, in which to place the captured pieces.
- Difficult to lift full board off the table.
- Difficult to place pegs into the holes
- Nowhere to put the pegs when not in use.
Preliminaries
Board Notation and Identification
Because each board location is
generally marked by a depression or hole, in which the marble or
peg sits, we often refer to a board location as a hole.
We need some kind of notation to identify the holes in the board.
On the cross-shaped 33-hole board the most common notation
is to label the board columns a-g (left to right) and the rows 1-7
(top to bottom).
This notation is familiar to chess players,
although note the minor difference that traditionally rows are numbered top to bottom.
This notation works well for any peg solitaire board that fits inside a 7x7 square,
and is referred to as "Standard 7x7 Notation" (see below, left).
We mention quickly other possible notations:
first, one can simply number the holes consecutively.
This notation is quite common,
the main problem with it is that the numbering changes every time the board shape changes.
John Conway invented an alphabetic notation which mirrors
the symmetry of the board [B3].
The most general notation is 2D Cartesian coordinates,
with the origin at the center of the board (to preserve symmetry),
or perhaps at the lower left corner (to avoid negative coordinates).
This notation (see below, right) is bulky and is primarily used in computer programs.
|
|
 |
 |
 |
 |
 |
|
|
|
|
 |
c1 |
d1 |
e1 |
 |
|
|
 |
 |
 |
c2 |
d2 |
e2 |
 |
 |
 |
 |
a3 |
b3 |
c3 |
d3 |
e3 |
f3 |
g3 |
 |
 |
a4 |
b4 |
c4 |
d4 |
e4 |
f4 |
g4 |
 |
 |
a5 |
b5 |
c5 |
d5 |
e5 |
f5 |
g5 |
 |
 |
 |
 |
c6 |
d6 |
e6 |
 |
 |
 |
|
|
 |
c7 |
d7 |
e7 |
 |
|
|
|
|
 |
 |
 |
 |
 |
|
|
|
|
|
|
 |
 |
 |
 |
 |
|
|
| y= 3 |
|
|
 |
|
|
|
 |
|
|
| y= 2 |
 |
 |
 |
|
|
|
 |
 |
 |
| y= 1 |
 |
|
 |
|
 |
|
 |
|
 |
| y= 0 |
 |
|
|
 |
|
 |
|
|
 |
| y=-1 |
 |
|
|
 |
 |
 |
|
|
 |
| y=-2 |
 |
 |
 |
|
|
|
 |
 |
 |
| y=-3 |
|
|
 |
|
|
|
 |
|
|
|
|
|
 |
 |
 |
 |
 |
|
|
| x= |
|
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
|
Standard 7x7 Notation
[used by Beasley]
|
The bulky but general alternative:
Cartesian Coordinates
|
|
For larger boards, "Standard 7x7 Notation" must be extended.
"Standard 9x9 Notation" is the obvious extension,
where the columns are a-i and the rows 1-9
(the most interesting boards have an odd width, and that is
why we go from 7x7 to 9x9).
An unfortunate aspect of this notational switch is that the central hole
goes from being called "d4" to "e5".
In standard 7x7 notation, to refer to a jump we simply list the
starting and ending board locations separated by a dash, i.e. "e5-e3"
for one of the jumps available above,
and "e5-e3-c3-a3" for the move "e5-e3, e3-c3, c3-a3".

|
A hand carved board with clay marbles, dating from
the early 1900's (photo courtesy St. John Stimson).
|
Any hole on the board that cannot be jumped over is called a corner hole.
The standard board above has 8 corners: c1, e1, a3, g3, a5, g5, c7 and e7.
The number and geometry of the corners is an important aspect of any peg
solitaire board.
We will call a board gapless if for any two board locations
in the same row or column, all the intervening points are also on the board.
All of the boards on this page are gapless, and this concept is mainly useful
to exclude pathological boards with interior holes or gaps along the edge.
A board is called rectangular-symmetric if it is unchanged when reflected
about the x- or y-axes, and rotationally-symmetric if it is unchanged
by any 90 degree rotation.
A board is called square-symmetric if it is both rectangular-symmetric
and rotationally-symmetric.
Finally, a square-symmetric board with a unique central hole
is called odd because its width is odd, and it also
has an odd total number of holes.
We see that the board above is odd, square-symmetric and gapless.
Complement Problems and Single Vacancy to Single Survivor Problems
Given a board position, the complement board position is
obtained by replacing every peg by a hole (i.e. removing the peg) and
replacing every hole by a peg.
Although the concept of complement initially seems to have nothing to do with the game,
we will see that it is very important.
Notice that the goal of the central game
is to go from the starting board position to its complement,
this is by no means a coincidence.
The general peg solitaire problem is to play from a full board with one
peg missing to a board position where only one peg remains.
These problems are called single vacancy to single survivor problems,
sometimes abbreviated SVSS.
The special problem where the initial vacancy and survivor are the same board
location is called the (single vacancy) complement problem.
Position Class and Null-Class Boards
How do we know which single vacancy to single survivor problems are
potentially solvable?
This is answered very elegantly using parity arguments along the diagonals.
The arguments below have been "rediscovered" many times.
The earliest known reference goes back to 1842.
Mathematicians enjoy using group theory to derive these results; however the
simple parity arguments below suffice.
Consider a diagonal labeling of the board holes (in two ways) as shown below:
|
|
1 |
2 |
3 |
|
|
|
|
2 |
3 |
1 |
|
|
| 1 |
2 |
3 |
1 |
2 |
3 |
1 |
| 2 |
3 |
1 |
2 |
3 |
1 |
2 |
| 3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
|
3 |
1 |
2 |
|
|
|
|
1 |
2 |
3 |
|
|
|
|
|
4 |
5 |
6 |
|
|
|
|
6 |
4 |
5 |
|
|
| 6 |
4 |
5 |
6 |
4 |
5 |
6 |
| 5 |
6 |
4 |
5 |
6 |
4 |
5 |
| 4 |
5 |
6 |
4 |
5 |
6 |
4 |
|
|
5 |
6 |
4 |
|
|
|
|
4 |
5 |
6 |
|
|
|
|
Given a board position B,
let Ni(B) be the number of pegs in the cells marked i,
and T(B) be the total number of pegs on the board.
Now consider what happens to these functions after a solitaire jump is executed.
The total number of pegs T always goes down by one, while one of
N1, N2 or N3
increases by one while the other two decrease by one
(and similarly for N4, N5,
N6).
Therefore the evenness or oddness of the differences T-Ni
does not change as the game is played.
This partitions the set of all possible boards into
sixteen position classes depending on the parity (even or oddness)
of the six numbers:
(T-N1,T-N2,T-N3,T-
N4,T-N5,T-N6).
As you play solitaire you cannot leave the position class that you start in.
[You might think there should be 26 or 64 position classes.
However the numbers Ni are not independent, because
T = N1+N2+N3 =
N4+N5+N6,
and this implies that among (T-N1,T-
N2,T-N3),
there are either zero or two odd parities (and similarly for the other half)
and the number of position classes is reduced to 24 or 16].
At the standard starting position with only the center hole vacant,
you can easily check that
N1=N3=N4=N6
=11,
N2=N5=10,
and the total number of pegs T=32.
Therefore the 6 starting parities (T-Ni), i=1,2, ... 6
and therefore
the position class of the board is (Odd, Even, Odd, Odd, Even, Odd).
All board positions reachable from
this starting position must be in this same position class.
The position class of a board position with only a single peg is easy to
calculate,
it is odd on all diagonals except for the two the peg is in.
Hence we see that the only possible finishing locations for the game must
be the intersections between diagonals 2 and 5, or the board locations
(0,0)=d4, (3,0)=g4, (0,3)=d1, (-3,0)=a4 or (0,-3)=d7.
Consider the board position with every hole filled by a peg.
Then T=33, Ni=11 for all i, and all six
parities are Even.
The empty board with no pegs also lies
in the same position class: (Even,Even,Even,Even,Even,Even).
This is the defining property of a null-class board: any board position
and its complement are always in the same position class (the
complement
of a board position is the board position where each peg is replaced by a hole
and vice versa).
It is important to realize that null-class boards are special, and not all boards
are null-class boards.
By using the parity argument above, one can easily prove the following
two facts about null-class boards:
-
Only on a null-class board is it possible to solve the complement problem.
-
Consider a null-class board with an initial vacancy at
(x0,y0).
Then we can only finish with a single peg at
board positions (x1,y1) where the differences
x1-x0 and y1-y0 are multiples of 3.
This is referred to by John Conway et. al. as "the rule of three"
[B3].
Even on a null-class board, it is important to realize that the above
conditions do
not guarantee that a particular single vacancy to single survivor problem
can be solved (they are only necessary conditions).
What can we say if a board is not a null-class board?
We know that no complement problem is solvable, for starters.
Some single vacancy to single survivor problems may still be solvable,
but generally
only a few.
For details on all of this, see Beasley's book [B1].
From a practical standpoint, how do we determine whether a particular board
is null-class or not? The most obvious technique is to label the board in the
above fashion and count the number of 1's, 2's, 3's through 6's.
If these six numbers have the same parity (all odd or all even) then the board
is null-class, otherwise it is not.
A more clever technique is to apply local transformations to the full board
that do
not change the position class we are in, and try to reduce it to the empty
board.
A simple class of very useful transformations is to
take the complement of any three consecutive board locations
(vertically or horizontally).
A solitaire move itself is such a transformation, but there are others, such
as removing three pegs in a row,
or replacing two pegs separated by a hole by a peg in the hole.
Using this technique we can discover which position
class any pattern of pegs is in, and which finishing holes are possible.
Short Solutions
 A jump is by definition a single jump of one peg over another.
When the same peg jumps one or more pegs, we call this one move.
The following terminology is useful in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep
(clearly, this terminology is only useful when n > 1).
A sweep that begins and ends at the same board location
is called a loop (or an n-loop).
A jump is by definition a single jump of one peg over another.
When the same peg jumps one or more pegs, we call this one move.
The following terminology is useful in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep
(clearly, this terminology is only useful when n > 1).
A sweep that begins and ends at the same board location
is called a loop (or an n-loop).
On the left we see a board position on Wiegleb's board
from which a remarkable 16-loop can be executed.
This loop move fits on the English Board,
however on Wiegleb's board this board position can actually be reached in a
single vacancy to single survivor game.
An interesting puzzle which can be solved by hand is to
find a solution with a 16-loop.
Playing Backwards
After attempting a peg solitaire problem,
many people get the idea to try to solve it backwards starting from a one-peg position.
What is not at all obvious is that this is exactly the same as the original game,
only with the concepts of "hole" and "peg" interchanged
(see [B3]).
In fact, the solution to any peg solitaire problem actually contains two solutions:
the original "forward" solution plus a hidden "backward" solution,
where the individual jumps are executed in the same direction,
but in reverse order
(and the starting vacancy and finishing location are swapped).
For a complement problem,
this means the backward solution is a second (different)
solution to the same puzzle.
Backward play is hard to comprehend, because our brain does not easily
interchange the concepts of "hole" and "peg".
It is hard to shake the perception that a hole is the absence of a peg.
It is much easier to understand "backward play" by realizing that it is the
same as forward play from the complement of the current board position.
 For example, suppose we want to solve the puzzle mentioned above on
Wiegleb's board.
Namely, we want to find a solution beginning with one peg missing, and ending
with a spectacular 16-loop.
Playing forward, how can we possibly know which 27 jumps might end at the complex
17-peg pattern shown above?
It seems hopeless, even impossible;
but now we know that playing the game backwards from the 16-loop position
is the same as playing the game forward from the complement of this position.
So we begin from the complement of the 16-loop position
(shown on the left).
If we can solve this board to one peg
(and this is possible),
then the 16-sweep is ours!
We then begin with a board filled except for where this solution ended,
and play the jump sequence in reverse.
This will magically reproduce the 16-loop board position!
We will return to this puzzle later.
In [B3] this solving technique is called the
"time reversal trick",
and it can be a powerful tool for solving certain problems.
For example, suppose we want to solve the puzzle mentioned above on
Wiegleb's board.
Namely, we want to find a solution beginning with one peg missing, and ending
with a spectacular 16-loop.
Playing forward, how can we possibly know which 27 jumps might end at the complex
17-peg pattern shown above?
It seems hopeless, even impossible;
but now we know that playing the game backwards from the 16-loop position
is the same as playing the game forward from the complement of this position.
So we begin from the complement of the 16-loop position
(shown on the left).
If we can solve this board to one peg
(and this is possible),
then the 16-sweep is ours!
We then begin with a board filled except for where this solution ended,
and play the jump sequence in reverse.
This will magically reproduce the 16-loop board position!
We will return to this puzzle later.
In [B3] this solving technique is called the
"time reversal trick",
and it can be a powerful tool for solving certain problems.
Boards
The English "Standard" Board (33 holes)
 This board is justifiably popular,
and is the only peg solitaire board many people know of.
We just showed that this board is a null-class board.
A great deal can be proven about this board without the aid of a computer.
The book by John Beasley [B1]
is the authoritative reference and highly recommended.
A more general reference that is easier to find is
Winning Ways For Your Mathematical Plays [B3].
This four volume set was republished in 2004;
Volume #4 is the one to buy because it contains the peg solitaire
chapter: "Purging Pegs Properly".
This board is justifiably popular,
and is the only peg solitaire board many people know of.
We just showed that this board is a null-class board.
A great deal can be proven about this board without the aid of a computer.
The book by John Beasley [B1]
is the authoritative reference and highly recommended.
A more general reference that is easier to find is
Winning Ways For Your Mathematical Plays [B3].
This four volume set was republished in 2004;
Volume #4 is the one to buy because it contains the peg solitaire
chapter: "Purging Pegs Properly".
Over the years,
literally hundreds of versions of this board have been produced under brand names such as
Puzzle Pegs,
Hi-Q,
and Classical Solitaire.
Even today, if you google
peg solitaire board
you will find dozens of English boards to choose from.
The most expensive boards, with exotic marbles, for some reason usually include the four
extra holes of the French Board.

|
|
Screen capture of "Pegged".
|
The computer puzzle "Pegged" was included in
Microsoft Windows 3.0 (1990),
one of eight puzzles in the first
Microsoft Entertainment Pack.
Why is the English board so popular?
It is the smallest
square-symmetric,
gapless board on which
the central game is solvable (see [P3]).
In fact, it is the smallest such board on which every
complement problem is solvable.
Ernest Bergholt found an
18-move solution to the
central game in 1912.
In 1964, John Beasley proved that there is no shorter solution
to the central game [B1].
Since then the problem of finding minimal length solutions has been attacked by many
people using a computer, and minimal length solutions to all
single vacancy to single survivor problems have been found.
In 2012, Joseph Barker and Richard Korf [P8] applied
advanced search techniques
to this problem—their search algorithm can find Bergholt's solution
using less than 3 seconds of CPU time!
They can find shortest solutions to all 21 SVSS problems
using less than 2 minutes of CPU time [P8].
Over the years, there have been various attempts to describe a solution to the
central game that is easy to remember.
Bergholt's 18-move solution is shortest, but tends to be difficult to recall.
Nonetheless, a specialized "Wolstenholme notation" has been invented to assist in recalling it
[W19].
Another solution, called "Jabberwockey", is given in Martin Gardner's book
[B2].
This solution has some nice symmetry properties, which make it easier to remember, as
well as faster because one captures pegs with both hands simultaneously
during the solution.
Click here to see a diagram of this solution
(paired moves are shown in red).
|
|
|
c1 |
d1 |
e1 |
|
|
|
|
c2 |
d2 |
e2 |
|
|
| a3 |
b3 |
c3 |
d3 |
e3 |
f3 |
g3 |
| a4 |
b4 |
c4 |
d4 |
e4 |
f4 |
g4 |
| a5 |
b5 |
c5 |
d5 |
e5 |
f5 |
g5 |
|
|
c6 |
d6 |
e6 |
|
|
|
|
c7 |
d7 |
e7 |
|
|
|
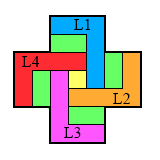
My personal favorite easy to remember solution to the central game
requires that you memorize the L-move (see [W2] under L-Package).
Start with d2-d4, f3-d3, and now focus in on the (blue) L-shaped region
defined by L1={e4, e3, e2, e1, d1, c1} (see the diagram on the left).
The L-move consists of three moves (four jumps) whose net effect is to complement or reverse
the state of the pegs in L1: e1-e3, e4-e2, c1-e1-e3
(or you can do e1-e3, c1-e1, e4-e2, e1-e3 if you find this easier to remember).
We now do the L-move on the other three arms of the cross.
First, e6-e4 to open up (orange) L2={d5, e5, f5, g5, g4, g3}, then the second L-move:
g5-e5, d5-f5, g3-g5-e5.
Next, b5-d5 to open up (purple) L3={c4, c5, c6, c7, d7, e7}, then the third L-move:
c7-c5, c4-c6, e7-c7-c5.
Finally, c2-c4 to open up (red) L4={d3, c3, b3, a3, a4, a5}, then the last L-move:
a3-c3, d3-b3, a5-a3-c3.
This leaves you in the board position shown on the upper right.
Notice the six jump loop starting from d5: d5-b5-b3-d3-f3-f5-d5.
This leaves the board with a "T" shaped configuration of pegs on the right
which can be solved (by inspection):
d4-f4, d6-d4, c4-e4, f4-d4.
The animation on the right shows the whole solution, or see
this diagram, or this
WikiHow Page
[W21].
Note also that the screen capture of "Pegged", above left,
also seems to be from the middle of such a solution.
To obtain the board position in the screen capture,
you have to reflect the board about the x-axis.
So the opening move was d6-d4 (not d2-d4),
and the screen snap is taken during the jump c4-c2 (c4-c6 in the previous paragraph).
If diagonal jumps are allowed, what is the shortest solution to
the central game?
In Beasley's book [B1] he gives a 16-move solution,
and remarks that it is not known if this is the shortest.
In 2006, I was able to complete the exhaustive search,
and the shortest solution has
15 moves
[P4].
 A web page on the shortest solution when
diagonal jumps are allowed.
A web page on the shortest solution when
diagonal jumps are allowed.
 A web page with sample computer calculations for the English 33-hole board.
A web page with sample computer calculations for the English 33-hole board.
The 6x6 Board (36 holes)
 This 36-hole board is the smallest square board on which a
complement problem is solvable.
It is the second smallest
square-symmetric, gapless board on which every
complement problem is solvable
(see [P3]).
In general it is less interesting than the English board, because
it lacks a central hole and has a simpler geometry.
It does, however, support some remarkably short solutions.
John W. Harris and Harry O. Davis studied this board in the 1960's, and found that most
single vacancy to single survivor problems can be solved in
15 moves,
with a few cases requiring 16 moves [W1].
This 36-hole board is the smallest square board on which a
complement problem is solvable.
It is the second smallest
square-symmetric, gapless board on which every
complement problem is solvable
(see [P3]).
In general it is less interesting than the English board, because
it lacks a central hole and has a simpler geometry.
It does, however, support some remarkably short solutions.
John W. Harris and Harry O. Davis studied this board in the 1960's, and found that most
single vacancy to single survivor problems can be solved in
15 moves,
with a few cases requiring 16 moves [W1].
This board does have one unusual property: it is possible for any peg on the
board to reach some corner.
No matter where the final peg is to be left, it is possible
to arrange things so that the last four moves start from the four corners.
If this board is easy for you try finding solutions with this property.
Click
here to see an elegant
15-move solution with this property, due to John Harris [W1].
Here is another one I found.
It is not always possible to have a minimal length solution with this
corner finish property.
A double vacancy complement problem
is a puzzle where two pegs are removed at the start,
and your goal is to finish with two pegs in the original vacancies.
On the 6x6 board, all 93 double vacancy complement problems are solvable
(unlike the English 33-hole board,
where four double vacancy complement problems are not solvable
[B1, p. 106-9]).
It is tedious to find solutions for the 93 cases,
but all are solvable (here is a
sample solution).
The 6x6 board is not the smallest board where all double vacancy complement problems are solvable,
the 6x4 rectangular board also has this property.
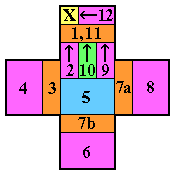
The French Board (37 holes)
 This was the first peg solitaire board, appearing in France in the late 17th century.
In Winning Ways For Your Mathematical Plays [B3]
it is referred to as the "Continental Board".
Antique French boards are usually paddle-shaped with a handle,
as shown on the right (see also the
board in the 1697 engraving).
Traditionally, the pegs are ivory, but have a tendency to become lost.
This was the first peg solitaire board, appearing in France in the late 17th century.
In Winning Ways For Your Mathematical Plays [B3]
it is referred to as the "Continental Board".
Antique French boards are usually paddle-shaped with a handle,
as shown on the right (see also the
board in the 1697 engraving).
Traditionally, the pegs are ivory, but have a tendency to become lost.
This board is not a null-class board, therefore no
complement problem is solvable on it.
Using the position class theory,
one can prove that if you begin from a filled board with only the center vacant,
it is impossible to finish with one peg, anywhere.
To show this, simply compute the six parities of the starting board position.
All six parities are even, and therefore all six parities will always be even.
But any one peg position has four odd parities and two even parities,
so no single peg position can be reached.
Nonetheless, there are ten single vacancy to single survivor problems
solvable on this board, and
each can be solved in 20 or 21 moves.
If you are solving a problem by hand, the best technique to use
(on any board) is to decompose it into block removals.
Note that the French board decomposes nicely into L and 3-removals
as shown on the right.
In order to solve a particular problem, one can modify this diagram
with appropriate starting and ending moves, as shown on the left.
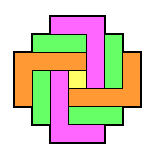
In each diagram, the location of the starting hole is marked by an "S",
and the finishing hole by an "F".
After dividing the board up into block removals,
one must also check that the catalyst needed by each block removal
is present.
The sequencing of the block removals is indicated by the numbering.
If you don't understand how to turn such a diagram into a solution,
read the introduction to block removals at [W2].
If the game begins with the center peg missing, this board position
is in the position class of the empty board,
so it is not possible to finish with one peg.
An interesting modification of the rules which allows for a d4 to d4 solution
is known as Cremers' Key
[W16].
According to [W16],
this concept was invented around 1998 by Frans Cremers,
a retired teacher from Aalter, Belgium.
Play proceeds from the center as normal,
but the player is allowed to replace the
central peg once when the hole is unoccupied.
This puts the board position in the correct
position class,
and a solution can be obtained.
The shortest solution to the central game using Cremers' Key has
20 moves.
Note that Cremers' key works not only from the center start, but from any start.
In the general case one is allowed to replace the peg at the starting hole once.
The goal is to finish with one peg,
not at the starting location, but always in the center.
The reason why this works is clear if you understand position classes.
On the French board, the board with every hole filled by a peg is in the same position class as
the board with one peg in the center.
Therefore, when you replace a peg at the starting hole, what you are doing is changing
the position class to that of the full board, so that finishing in the center is now possible.
The results of [P3] show
that Cremers' Key will put the board in the
position class
of the center finish on any gapless,
odd,
square-symmetric
board that is not null-class.
Another way to make the central game solvable is to allow diagonal jumps.
In this case the central game can be solved in as little as
13 moves.
One interesting puzzle with diagonal jumps is to begin with pegs
at all locations except for the central 9 holes
{c3, c4, c5, d3, d4, d5, e3, e4, e5}, and try to
play to the complement of this position
with only the center 9 holes occupied.
Allowing diagonal jumps, this "big central game" is solvable, but
the same problem is not solvable on the 33-hole
English board.
The shortest possible solution to the "big central game" has
13 moves.
One reason the "big central game" is interesting is that using it one can solve any
SVSS problem
[P4].
 A web page on the shortest solution when diagonal jumps are allowed
A web page on the shortest solution when diagonal jumps are allowed
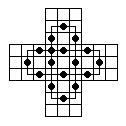
The 41-Hole Diamond Board
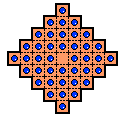 This board, sometimes called the "Continental" Board [B3],
can be traced back to
Édouard Lucas in 1882
[B1].
This is not a null-class board, and there are only
four single vacancy to single survivor problems
solvable on it (as shown in [B1]).
This board is very difficult to play on because it has 16
corners,
but for a computer solver this is a significant constraint on play.
All four single vacancy to single survivor problems on this board
can be solved in 26 moves, but no fewer [P2].
To view solutions, see the
solution catalog.
There exist
26 move solutions with a 9-sweep,
which is rather remarkable given
all the corners on this board.
This board is not easy to decompose into block removals.
In his book, Beasley
[B1] shows how to accomplish the task using more
complex block removals to deal with all the corners.
This board, sometimes called the "Continental" Board [B3],
can be traced back to
Édouard Lucas in 1882
[B1].
This is not a null-class board, and there are only
four single vacancy to single survivor problems
solvable on it (as shown in [B1]).
This board is very difficult to play on because it has 16
corners,
but for a computer solver this is a significant constraint on play.
All four single vacancy to single survivor problems on this board
can be solved in 26 moves, but no fewer [P2].
To view solutions, see the
solution catalog.
There exist
26 move solutions with a 9-sweep,
which is rather remarkable given
all the corners on this board.
This board is not easy to decompose into block removals.
In his book, Beasley
[B1] shows how to accomplish the task using more
complex block removals to deal with all the corners.
This board is a member of a general class known as a draughtsboard.
Such boards are obtained by taking any square board, and labeling the
holes alternately as on a chess or checkers board. Then the board is
rotated 45 degrees and the black squares define the holes of the draughtsboard.
The 41-hole diamond board can be so obtained starting from a 9x9 square board.
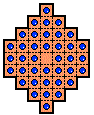 You can try to find a center to center solution using the
Cremers' Key [W16]
rule modification, but you will not succeed.
Replacing the center peg does give one a board position in the
correct position class,
but using the resource count
shown below one can prove that it is not possible to finish
with one peg.
You can try to find a center to center solution using the
Cremers' Key [W16]
rule modification, but you will not succeed.
Replacing the center peg does give one a board position in the
correct position class,
but using the resource count
shown below one can prove that it is not possible to finish
with one peg.
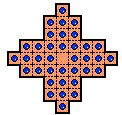 Several interesting variations to the 41-Hole Diamond Board have been proposed.
Around 1882, H.-A.-H. Hermary proposed removing the leftmost and rightmost holes
from the board, giving Hermary's 39-Hole board, shown on the right.
This board is null-class,
rectangular-symmetric,
and most (but not all) complement problems are solvable [B1].
The central game on Hermary's 39-hole board can be solved in
a minimum of 23 moves.
Several interesting variations to the 41-Hole Diamond Board have been proposed.
Around 1882, H.-A.-H. Hermary proposed removing the leftmost and rightmost holes
from the board, giving Hermary's 39-Hole board, shown on the right.
This board is null-class,
rectangular-symmetric,
and most (but not all) complement problems are solvable [B1].
The central game on Hermary's 39-hole board can be solved in
a minimum of 23 moves.
In 1894, A. Huber removed 4 holes to produce Huber's 37-Hole board, shown on the left.
This board is null-class and
square-symmetric—the central vacancy and other
complement problems are solvable.
The central game on Huber's 37-hole board can be solved in
a minimum of 20 moves.
We note that the complement problem at the "tip of the arm" is not solvable
(proved in [P3]).
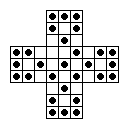
The 32-Hole Diamond Board
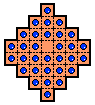
 This board is null-class and
rectangular-symmetric.
It is a draughtsboard created from an 8x8 square
board,
and a convenient way to play this board is using a checkers board,
playing only on the squares of one color with diagonal jumps.
In fact this board is identical to a standard checkers board,
just rotated 45 degrees, as the figure on the right shows.
This board is null-class and
rectangular-symmetric.
It is a draughtsboard created from an 8x8 square
board,
and a convenient way to play this board is using a checkers board,
playing only on the squares of one color with diagonal jumps.
In fact this board is identical to a standard checkers board,
just rotated 45 degrees, as the figure on the right shows.
This board has a similar size as the
standard English board, but it has 14
corners rather than 8.
In 1941, B. M. Stewart showed that all 25
SVSS problems
were solvable on this board.
My program has found that all of them are solvable in 17-19 moves,
with only the d1 (top hole) complement requiring
19 moves.
The d4-complement can be solved in
a minimum of 18 moves.
Hoppers Board


|
|
Cool Moves, 2007
|
Hoppers is a popular peg solitaire game invented by
Nob Yoshigahara and sold by
ThinkFun starting in 1999.
This peg solitaire board was patented 100 years earlier (1899) by William Breitenbach.
It is one of the first peg solitaire boards on which diagonal jumps were allowed
(and in fact required, for solving it).
The puzzle was available after 1899 in the USA under the name
The Great 13 Puzzle.
It has also been sold under the names
Target,
13 Peg Solitaire and
Birthday Solitaire.
In "Hoppers", Nob Yoshigahara came up with a whole set of challenge cards for this board.
He also had the idea of including a special red frog
which must be preserved and perform the final jump.
The original name for Nob's version was "Marsh Madness", as Bill Ritchie recounted in his
Memorial to Nob Yoshigahara
(in 2015 this link fails).
If you rotate this board 45 degrees, it is easy to see that it
is a 13 hole Diamond Board, or
draughtsboard created from a 5x5 square board,
with the addition of diagonal jumps along both diagonals.
Without the addition of diagonal jumps, no
single vacancy to single survivor problem
on this board is solvable.
However with the diagonal jumps many problems become solvable,
and its small size makes solutions easier to work out.
An interesting advanced problem is to try to solve the
central game on this board in as few as
7 moves.
 A web page with strategy tips for this board.
A web page with strategy tips for this board.
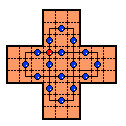
Wiegleb's Board (45 holes)

|
|
A Soli2 board.
|
This is one of the first boards to appear in print, in 1779 by J. C. Wiegleb.
It is a null-class board,
and also a Generalized Cross Board.
I have a board game called
Soli2 made by
Enginuity Games which is Wiegleb's Board
with four additional holes, with black and white marbles.
I haven't played Soli2 much,
but this is a convenient board for playing Wiegleb's Solitaire
(ignore the colors and the four extra holes).
There are 36 different SVSS problems on Wiegleb's Board,
all are solvable except for the (4,0) or e1
complement problem.
A proof that the (4,0) or e1-complement is unsolvable is not easy.
An outline of a proof is given in Beasley's book
[B1], but filling in the details is non-trivial
(I asked John Beasley about this, and he agrees that filling in the details is not easy).
I have found an alternate proof by integer programming
techniques [P3].
A computer proof by exhaustive search is possible, but time consuming.
 Trying to solve the (4,0) or e1-complement problem is several orders of magnitude
harder than any problem on the English board.
If you have a fast peg solitaire solver try testing it on this problem.
If you want to try a problem that actually has a solution,
try any other complement problem on this board,
or try the (4,0) or d1-complement problem on the 3232 Board.
Trying to solve the (4,0) or e1-complement problem is several orders of magnitude
harder than any problem on the English board.
If you have a fast peg solitaire solver try testing it on this problem.
If you want to try a problem that actually has a solution,
try any other complement problem on this board,
or try the (4,0) or d1-complement problem on the 3232 Board.
Problems on this board can be solved most easily using block removals
as shown on the figures to the left.
The numbering shows the ordering of the block removals.
Numbers subdivided a, b, c are block removals that must be interleaved,
in other words part b begins before part a is finished.
To see the sequence of moves, see the solution in
[W3].
Beasley [B1] gives block removal diagrams for
one other complement problem on this board.

|
Hand-made Wiegleb's Board in painted
plywood, 16 mm marbles,
DIY Puzzles.
|
The longest sweep possible on Wiegleb's board
has length 16—one possibility is shown on the board on the upper left.
Because it begins and ends at the same place, it is a 16-loop.
This sweep also fits on the English board,
but it cannot appear during a single vacancy to single survivor problem
(proved in Beasley's book [B1]).
In 2005, I discovered that on Wiegleb's board the 16-loop can
be reached [P2]!
There are three SVSS problems for which a 16-loop can occur.
Here is a web page
that you can print out to try these problems by hand:
- Vacate g4 (or equivalently d7), play to finish at d4 with
the last move a 16-loop (the above board shows the last move).
- Vacate g5, play to finish at d2 with the last move a 16-loop.
- Vacate d6 or g6, play to finish at d3 with the second to the last move a 16-loop.
The 16-loop begins and ends at d2.
You can go nuts trying to solve these playing forward.
The trick is to play backwards from the sweep position,
or equivalently play forward from the complement of the sweep position.
To read more about this trick and understand why it works,
read about the "time reversal trick" in the book
Winning Ways for your Mathematical Plays (Volume 4) [B3].
or see my description above.
No other combination of starting and finishing holes can contain a 16-sweep,
except of course rotations or reflections of the above three problems.
The three problems above can be solved in a minimum of
22, 24, and 23 total moves, respectively.
For solutions, see [P2] or
this web page.
The
solution catalog
shows the shortest length solution to all 35 solvable problems on this board,
an effort in 2004 which required 3 months of CPU time on a 1 GHz Pentium PC.
The results can be found in our paper [P2],
and in 2012 were confirmed by
Barker and Korf [P8].
All the problems are solvable in a minimum of 20-23 moves,
with only the (3,0) or e2 complement requiring
23 moves.
The central game can be solved in
22 moves, but no fewer.
There are a few problems on this board with unique minimal length solutions,
up to symmetry and move order.
For example, there is a unique
20 move solution from c4 to i4.
 A web page of computational results for Wiegleb's Board
A web page of computational results for Wiegleb's Board
 A web page on 16-loops on Wiegleb's Board
(print it out and try them yourself)
A web page on 16-loops on Wiegleb's Board
(print it out and try them yourself)
The 8x8 Board (64 holes)
 This board is not null-class, but may be conveniently
played on a checkers or chess board using 63 coins or poker chips.
You may begin with one peg missing at any of the locations marked on the left by an X
and (potentially) finish with one peg.
From any other start (for example, anywhere along the main diagonals)
a single peg finish is impossible.
This board is not null-class, but may be conveniently
played on a checkers or chess board using 63 coins or poker chips.
You may begin with one peg missing at any of the locations marked on the left by an X
and (potentially) finish with one peg.
From any other start (for example, anywhere along the main diagonals)
a single peg finish is impossible.
Using the same technique [W1] as for the 6x6 board,
it is easy to prove that the solution to any
SVSS problem
must have at least 24 moves.
 In 1986, John Harris found a
25-move solution
by hand [W1];
finding a shorter solution is a difficult computational task,
but in 2014 I found a 24-move solution
(and here is another).
In 1986, John Harris found a
25-move solution
by hand [W1];
finding a shorter solution is a difficult computational task,
but in 2014 I found a 24-move solution
(and here is another).
The longest finishing sweep on this board has length 21.
It is not difficult to find a solution finishing with a
21-sweep—this is a fun exercise to work out by hand.
As usual, you must begin from the complement of the sweep position
(one possibility is shown on the right).
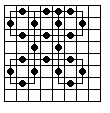
The 9x9 Board (81 holes)
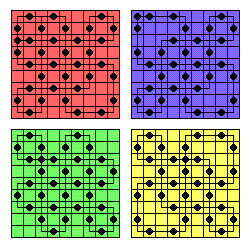 This board is null-class,
and all SVSS problems
are easy to solve using block removal methods.
The only physical board where it is possible to play 9x9 peg solitaire is a
Go board,
I recommend using a computer board [W20].
The 9x9 board supports some remarkably long sweeps, examples are shown to the left.
A sweep of 34 is the longest geometrically possible,
shown on the red board.
What is more remarkable is that this particular sweep
can be reached from a single vacancy start.
The other sweeps shown on the left are symmetrical 32-loops.
This board is null-class,
and all SVSS problems
are easy to solve using block removal methods.
The only physical board where it is possible to play 9x9 peg solitaire is a
Go board,
I recommend using a computer board [W20].
The 9x9 board supports some remarkably long sweeps, examples are shown to the left.
A sweep of 34 is the longest geometrically possible,
shown on the red board.
What is more remarkable is that this particular sweep
can be reached from a single vacancy start.
The other sweeps shown on the left are symmetrical 32-loops.
On this board, what is the shortest solution to the central game?
This is currently an open question.
In 2004, Alain Maye found a solution by hand in
34 moves.
It is likely that the shortest solution has around 30 moves, by analogy with the
10x8 board, which is of similar size.
Curiously, the odd side length makes the techniques used on the 10x8 board
much less powerful.
An interesting challenge is to demonstrate that the
32-loops shown to the left can be reached from single vacancy starts.
Some of them can also be the final move to a complement problem.
It is also possible to find a solution to the central game
ending with a 30-loop.
 A web page on the 9x9 board
A web page on the 9x9 board
Rectangular Boards and Even-Even Boards
A summary of even-even rectangular boards,
with links to shortest solutions.
|
An n by m rectangular board is null-class
if and only if n or m is a multiple of 3,
or equivalently if the total number of holes is a multiple of 3.
The 6x4 board is the smallest rectangular board where every
complement problem is solvable.
In fact, every double vacancy complement problem
is solvable on the 6x4 board
(where any two pegs are missing at the start, and one finishes with these two holes filled).
This is quite tedious to verify by hand,
but I have verified it by running my progam for all 78 cases.
The 6x4 board is probably the smallest board on a square grid
where all single and double vacancy complement problems are solvable.
Rectangular boards where both n and m are even
are more interesting than you might think,
we call them "even-even boards".
Why are even-even boards interesting?
By analogy with the proof [W1] on the 6x6 board,
it is easy to prove that the solution to any
SVSS problem
on an even-even board must have at least
(n/2+1)(m/2+1)-1 = nm/4+(n+m)/2
moves.
Therefore, if one can find a solution of this length,
it must be the shortest possible.
This may not sound very exciting,
but the remarkable thing is that it can be rather easy to find solutions of this length.
Even-even boards are interesting because it is surprisingly easy
to find the shortest solutions.
The grid to the left summarizes my results on even-even boards.
The green squares denote null-class boards,
otherwise the square is red.
Square boards appear along the diagonal.
The tiny 4x4 board has a minimum solution length of 8 moves,
an 8 move solution does not exist,
although 9 moves is possible.
For all larger even-even boards,
the minimum solution length seems to be attainable.
On the 6x4 board it is not difficult to find
11-move solutions, and
we have already mentioned that the 6x6 board has 15-move solutions.
On the 8x6 board, I have found
19-move solutions,
and on the 8x8 square board,
24-move solutions.
All of these are automatically the shortest possible, by the above argument.

|
|
67-hole Siege Board, ca. 1880
|
In 2014, I found a 29-move solution on the 10x8 board!
In 2015, I found a 34-move solution on the 12x8 board!!
This is the largest board (96 holes!) for which a solution having minimal length is known.
Finding these shortest solutions on such large boards requires advanced search techniques,
I use A* search
based on the number of filled Merson regions [B1].
The "Siege" Board (67 holes)
This board appeared in England around 1880, and has two unusual properties.
First, two additional holes have been added to the top
row (breaking the square symmetry).
Second, a set of holes is outlined in green.
Robert Reid has emailed me that this board is in David Parlett's
Oxford History of Board Games (p. 192),
and that the markings are for
a Fox and Geese
variant called "Siege".
He doubts this board was ever used to play peg solitaire.
Generalized Cross Boards
The 33-hole board can be thought of as a 3x3 "core" attached to
four 2x3 "arms".
One can generalize this concept by starting with the core
and adding four arms of size ni x 3.
Because they are built up from rows of three, these are all
null-class boards.
The board on the upper left is the only one which has been sold under the name
I.Q. Solitaire.
|
|
c1 |
d1 |
e1 |
|
|
|
|
c2 |
d2 |
e2 |
|
|
|
|
c3 |
d3 |
e3 |
|
|
| a4 |
b4 |
c4 |
d4 |
e4 |
f4 |
g4 |
| a5 |
b5 |
c5 |
d5 |
e5 |
f5 |
g5 |
| a6 |
b6 |
c6 |
d6 |
e6 |
f6 |
g6 |
|
|
c7 |
d7 |
e7 |
|
|
|
|
c8 |
d8 |
e8 |
|
|
|
|
c9 |
d9 |
e9 |
|
|
|
I investigated these boards in 2003 and found there are exactly
12 generalized cross boards where the
complement problem
is solvable at every board location.
Of these 12, the only board with square symmetry is the
standard 33-hole board.
Two have rectangular symmetry
(top row of figure to the left),
three have mirror symmetry about one axis,
two have diagonal symmetry (second row) and the remaining
four have no symmetries at all.
Of particular interest is the 39-hole board in the upper right
with alternating arm lengths 3,2,3,2.
Our hole notation for this board is shown to the right.
A very hard problem is to solve the d1-complement problem.
The solution to this complement problem is unique
up to symmetry and move order [P2].
This is an unusual property for a peg solitaire solution
and makes this puzzle hard to solve,
either by hand or using a computer.
Try this problem yourself using
this online puzzle.
Here are four challenges of increasing difficulty on the "3232 Board".
- Find a solution to the central game (d5-complement).
- Find a solution to the a4-complement ending with the 12-loop:
a4-c4-c2-e2-e4-g4-g6-e6-e8-c8-c6-a6-a4.
- Vacate a4, and mark the man at g4. Play to finish at a4 with the marked man sweeping off 13 in the final move.
- Find a solution to the d1-complement. Hard!
 A web page on Generalized Cross Boards
A web page on Generalized Cross Boards
 Coming ... A web page with 4 challenges on the 3232 Board
(print it out and try them yourself)
Coming ... A web page with 4 challenges on the 3232 Board
(print it out and try them yourself)

|
A Solo Board. Photo courtesy
Jaap Scherphuis [W20].
|
Kralenspel or Solo Board
This heart-shaped 41-hole board is of Dutch or Swedish origin, I believe;
the name translates from Dutch as "bead game".
It is commonly known by the trade name "Solo".
The most interesting aspect of these boards is that instead of pegs they use beads or marbles
which are white on one side, and black on the other.
Instead of jumping pegs, the three marbles involved are rolled.
Solo boards are perhaps the only peg solitaire boards where the
game pieces are not removed as jumps are performed.
Another copy can be found in
item #3529 of the Jerry Slocum collection
[W22].
The Solo board is not null-class.
For detailed analysis of this board see
this web page
on Jaap's Puzzle Page [W20].
Triangular Boards
All the boards above are based on a square lattice.
One can also play peg solitaire on a triangular lattice.
As noted in Beasley [B1], solitaire on such a lattice
is equivalent to solitaire on a square lattice with the addition of
moves along one diagonal.
 There is now a separate web page for Triangular
Solitaire.
There is now a separate web page for Triangular
Solitaire.
General Boards
At this point we leave the "normal" peg solitaire boards,
and consider ways the puzzle can be generalized.
If we generalize too far, an interesting phenomenon occurs.
Namely, it becomes possible to start with any peg missing,
and play to finish with one peg at any other hole
(the rule of three goes out the window).
We will call a board with this property universal
(with respect to these jumping rules).
We have already seen that many boards become universal
when diagonal jumps are allowed [P4],
we will see more univeral boards below.
Jumping rules leading to a universal board indicate a fundamental change
in the game—the position classes
have "collapsed" into a single set,
really the whole concept of a position class becomes meaningless.
Since every board position is in the same position class,
all boards are null-class
(this term has also become meaningless).
A universal board sounds like a good thing,
but in reality it is an indicator that the puzzle will be confusing.
At least, a universal board seems far removed from "standard" peg solitaire,
where one can rely on the comfortable rule of three.
Consider, for example, the English Board.
From a randomly chosen board position (probability of 1/2 to have a peg in any hole)
there are an average of 9.5 jumps available.
If diagonal jumps are allowed, the board becomes universal,
and the average number of jumps almost doubles to 17.0.
From experience, it seems too difficult to consider 17 possible jumps.
This suggests the total number of board positions which
can be reached after 5 jumps is about 175,
which is more than one million.
In contrast, under normal jumping rules only around 77,000 board positions
should be reachable after 5 jumps.
Gridless Boards
 Peg solitaire need not be played on a regular grid.
In principle it can be played on any network of intersecting lines
(or even an
arbitrary graph [P7]
if one allows jumps along any triple of connected nodes).
We call boards which are not based on a regular (square or triangular) grid "gridless".
Our derivation of null-class
does not extend to gridless boards; however,
the concept can sometimes be extended using "invariant parity counts",
as explained in Beasley's book
[B1, p. 63-5 and p. 241-2].
Several examples of invariant parity counts are given below.
Peg solitaire need not be played on a regular grid.
In principle it can be played on any network of intersecting lines
(or even an
arbitrary graph [P7]
if one allows jumps along any triple of connected nodes).
We call boards which are not based on a regular (square or triangular) grid "gridless".
Our derivation of null-class
does not extend to gridless boards; however,
the concept can sometimes be extended using "invariant parity counts",
as explained in Beasley's book
[B1, p. 63-5 and p. 241-2].
Several examples of invariant parity counts are given below.
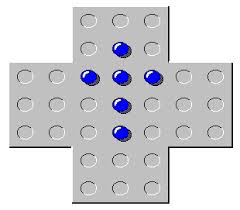
The most common gridless board seems to be Star Jump (shown to the left), a 10-hole board sold by
Creative Crafthouse,
it has also been sold under the names
Penta,
Star Solitaire,
and Star Trekker.
One marble is removed at the start and this puzzle uses normal peg solitaire
rules, with jumps allowed along the lines on the board.
As usual, the goal is to finish with one peg.
If we let p0 be the parity (even or odd) of the number of pegs in the outer ring,
and p1 be the parity for the inner ring.
A peg solitaire jump always changes p0 and never changes p1.
Since a solution contains an even number of jumps (eight),
both parities must be the same for the starting and ending board positions.
If we start with a vacancy in the outer ring, we can only finish in the inner ring,
and vice-versa.
Over the years, many gridless boards have been devised.
Solomon
was invented by Martin Gardner in the 1960's as a two player game,
and can also be used for peg solitaire.
This 19-hole, star shaped board be be purchased at
Kadon Enterprises.
Related to both Solomon and Star Jump is a 16-hole board
based on a 5-pointed star [B1, p. 242-3].
Some gridless boards have no corners,
a property which we have not seen to this point.
Hyper Solitaire
is a 33-hole English board
which has been warped so that jumps can be made "around the corners".
Although there are 108 possible jumps,
Hyper Solitaire is not universal,
as shown by the following argument:
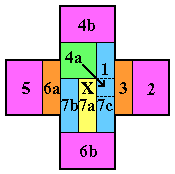
consider the 12 hole set R marked in red on the photo to the left.
We note that there is no jump which can add or remove one peg from R
(pegs can only be removed from R in pairs).
Therefore, the parity of the number of pegs in the set R can never change.
Thus if the initial vacancy is in R, you can only finish in R,
and if you start outside R, you can only finish outside R.
Round Solitaire
is a modification of Hyper Solitaire invented in 2009 by Tetsuro Kawahara,
he removed the outer ring of 12 holes.
The central game is solvable on this board in a minimum of 8 moves.
Round Solitaire is not universal [P10],
this can be demonstrated using the set R of the previous paragraph.
This is just a sampling of gridless boards,
additional examples can be found in Beasley's book [B1],
or his more recent update article [P10].
Doughnut Solitaire or Toroidal Solitaire
Legal jumps in 4x4 toroidal solitaire
|
| a1 |
b1 |
c1 |
d1 |
| a2 |
b2 |
c2 |
d2 |
| a3 |
b3 |
c3 |
d3 |
| a4 |
b4 |
c4 |
d4 |
Notation
|
An 8-sweep?
|

A 5-move solution to the a1-complement!
|

|
|
A toroidal chess board!
|
We can play peg solitaire on a doughnut or torus,
the easiest way is to use a
rectangular board and identify opposite edges.
A jump which ends "off the board" is legal, provided the finishing hole is empty.
See the sample jumps on the 4x4 board to the left.
We'll refer to a board with opposite edges identified
as a board under "toroidal jumping rules".
Unlike chess moves, peg solitiare jumps are localized,
so executing jumps "across an edge" is easy,
once you get the hang of it.
However, understanding the effect of these new jumps on the game requires some thought.
Consider, for example, the 4x4 board.
Under normal peg solitaire rules, this board isn't very interesting,
the only SVSS problems which are solvable have the form:
vacate a2, finish at a3 (or d3).
Under toroidal jumping rules, the board becomes universal.
The symmetry of the board is also very different:
there are no corners or edges—all holes are the same.
The red graphic to the left shows a curious 8-loop on the 4x4 toroidal board.
Unfortunately, it cannot be reached from any single vacancy start.
My program has found that all SVSS problems on this board
can be solved in a minimum of 5 moves (see the example solution to the left).
It is remarkable that the first move can be a double jump!
The reader may enjoy demonstrating that the central game on 3x3 toroidal solitaire
is solvable.
In fact, it is difficult to lose this game, is there any dead end?
An analysis of n by m rectangular boards under toroidal jumping rules
shows that if n and m are both multiples of 3 the board
is still null-class and the
"rule of three" still applies.
If both n and m are not multiples of 3,
the board is probably universal.
A simple extension of
the rule of three can give us this,
because by wrapping around the board any pair of holes can be considered
to have coordinates a multiple of 3 apart, as long as
n and m are not multiples of 3.
If one of n and m is a multiple of 3 and the other is not,
then we have an intermediate case where the rule of three
applies in only one dimension (the one divisible by 3).
My program has found that the shortest solution to the complement problem
on the 5x5 toroidal board has 8 moves,
and on the 6x6 toroidal board,
11 moves.
Starting from any rectangular board,
we can also identify opposite edges in other orientations to play
peg solitaire on a cylinder,
Möbius strip,
or Klein bottle.
It is not clear if these geometries have any more to offer than the torus.
 A proof that the 4x4 toroidal board is universal.
A proof that the 4x4 toroidal board is universal.
3D Solitaire
All boards above are 2D, why not play peg solitaire in 3D?
This, of course, is possible and was coined "Solidaire" by Harry O. Davis in 1965.
One difficulty is in creating a game board,
the computer could conceivably be useful here.
In 3D Solitaire the number of position classes increases to 256.
This peg solitaire variant is discussed in
Beasley's book [B1, Chapter 13],
look there for more information.
Online Puzzles
|
"Pegged", an early computer
version of peg solitaire.
|
One of the first computer peg solitaire games was "Pegged",
which was included in the
Microsoft Windows 3.0 Operating System (1990).
Sadly, this classic version of the game has disappeared from
modern Windoze machines—but no matter, peg solitaire is now ubiquitous on the web.
Most computer versions of peg solitaire have the ability to take back moves,
all the way back to the beginning if necessary.
In my opinion, this tends to make a puzzle seem easier,
compared with solving on a mechanical board.
Resetting the board is also trivial for a computer puzzle.
Computer versions of peg solitaire can also include demos or solutions,
and they can point out bad or good jumps.
Here are links to online peg solitaire puzzles I have created.
You must have JavaScript activated in your browser to play them.
Square grid peg solitaire boards:
Triangular peg solitaire boards:
I have also designed the (hexagonal) levels of a free online peg solitaire game.
You will need to download
Shockwave
to use it.
Thanks to Rob Gordon of
Article19 for the GUI.
Solution Catalogs
Here is a compilation of shortest length solutions for six of the boards introduced above.
These were calculated by exhaustive computer search.
If you want to know how this was done, see the
Computational Search Techniques
section that follows.
Given a board and a (solvable)
single vacancy to single survivor problem, there is
a minimum number of moves that can solve it.
These solutions have an elegant look to them and they tend to be extremely hard
to find by hand.
The table below shows a list of boards, together with some statistics about
each.
If you click on a board, you will see another table listing all single vacancy
to single survivor problems solvable on that board, together with information
about
these solutions.
These boards are square-symmetric
(except for Diamond32) and we only list unique
single vacancy to single survivor problems.
In other words, if one problem
can be obtained from another by rotation and/or reflection, only one will be
listed.
If you keep clicking on the tables, you can view
diagrams of minimal length solutions.
Some column heads you will see that require explanation:
- Number of Problems: This is the number of different solvable single
vacancy
to single survivor problems on this board (not including problems equivalent
by symmetry).
- Longest Sweep: The first column is the longest sweep possible in any
single vacancy to single survivor problem, regardless of solution length.
The second "Longest Sweep" column is the longest sweep possible in a
minimal length solution.
- Solution Lengths: This is the range in the number of moves in
the minimal length solutions, over all problems.
- Time to Calculate: This is the amount of CPU time that
was needed to calculate the underlying table (find all minimal
solutions to all problems).
Board Name
[click to see catalog] |
Number
of Holes |
Null-
Class?
|
Number
of Problems |
Longest Sweep
(any problem) |
Minimal Length Solution Properties |
| Solution Lengths |
Longest Sweep |
Time to Calculate |
 Diamond32
Diamond32
|
32 |
Yes |
35 |
8 or 9 |
17-19 |
8 |
2 hours |
 English
English
|
33 |
Yes |
21 |
9 † |
15-19 |
8 |
2 hours |
 6x6
6x6
|
36 |
Yes |
21 |
10 ‡ |
15-16 |
10 |
6 hours |
 French
French
|
37 |
No |
10 |
9 † |
20-21 |
9 |
24 hours |
 Diamond41
Diamond41
|
41 |
No |
4 |
9 |
26 |
9 |
3 hours |
 Wiegleb's
Wiegleb's
|
45 |
Yes |
35 |
16 ‡ |
20-23 |
14 |
3 months |
Table Footnotes: (†) From John Beasley's book [B1].
(‡) This is the longest sweep geometrically possible on this board,
and at least one such sweep
can be realized as the final move to a
single vacancy to single survivor problem.
|
The information in the above table has been calculated by other authors
in the case of the English, French and 6x6 boards.
My results have been checked against their results.
In 2012, Barker and Korf [P8]
confirmed my results for the 41-hole diamond and 45-hole Wiegleb's board.
Computational Search Techniques

|
Read the story
behind the creation
of this "very limited edition" board.
|
There are a number of techniques and programming tricks that can speed up
the search for minimum length solutions.
Many of these are primarily computer science concepts,
and I will mention only those ideas specific to peg solitaire.
A good introductory reference which has a nice progression of problems is
the 2007 book by Koetke [B4].
This book starts out with small boards that are easy to solve,
and discusses the problems encountered for larger boards.
It also has example programs in java.
This is one of the few peg solitaire references that contains a lot
of detail about solving the game computationally.
If you try to solve a peg solitaire problem in an inefficient manner your
program can take forever to run, even on the standard 33-hole board.
For example the most obvious technique is to store the sequence of moves
(or jumps) and try to exhaustively go through all possible sequences
(generally using a depth-first search).
Because there are a large number of move sequences that result
in the same board position, such an algorithm is extremely inefficient.
Somewhat surprisingly, this inefficient algorithm may still quickly
find a solution to the central game,
but we seek algorithms which perform well even in the worst case.
One significant improvement is to use a hash table or some other means to store board positions
seen previously so you do not have to investigate them farther.
A similar technique is to only keep track of the set of boards at
each level in the tree, rather than the moves.
I call this a search by levels.
This is much faster than a straight search over move sequences and can
solve any problem on the 33-hole board relatively quickly.
For boards larger than this, additional techniques are needed.
I have used four ideas to speed up a search by levels:
-
If the problem is symmetric, there is no need to search over solutions
that are really the same.
On the 33-hole English board this can help a lot for some problems
(for example the central game or d4 complement) but not on others
(for example the c1 complement).
- The use of resource counts or Pagoda functions as explained below (see
also [B1] or [B3]).
Whether this is useful computationally depends on the board as well as the
problem.
It is very helpful on the 41-hole Diamond Board.
- Search forward from the starting position and also backwards
from the desired final position, looking for matching board
positions in the middle.
This is known as a
bidirectional search.
A trade-off is that the programming is more complex.
See [P8].
-
A* search.
For examples of this algorithm applied to peg solitaire see
[P4]
and [P8].
Finally, one should be careful not to confuse the computer's
failure to find a solution with a proof that no solution exists.
These calculations are complex and lengthy,
particularly when resource counts, symmetry and forward/backward
calculations are all being used.
Logical bugs in the code can easily prevent the computer
from finding a solution, and much testing is required to make
sure the results are reasonable.
For example, no program that reports "no 17 move solution to the
English board central game" should be trusted unless it can find the
Bergholt solution in 18 moves.
You can also test your program by reproducing
these tables.
For details on computational search techniques see
[P4] and [P8].
Resource Counts
A resource count (sometimes called a Pagoda function) is a real valued
function on board states that cannot increase during play.
At first it may not be obvious that such functions exist, certainly only
very carefully chosen functions have this property.
The simplest (but least useful) example of a resource count has a value of +1
at all board locations. This function counts the number of pegs on the board
and decreases by one with every jump.
The most useful resource counts generally have negative values in
corners
(in fact, it is not hard to show that a resource count can only have
a negative value at a corner).
If a certain move leaves the board with a value that is less
than that of our final position, we know that this move cannot possibly lead
to a solution.
A very useful resource count on the 41-hole diamond board is:
|
|
|
|
 |
 |
 |
|
|
|
|
|
|
|
 |
 |
-1 |
 |
 |
|
|
|
|
|
 |
 |
-1 |
1 |
-1 |
 |
 |
|
|
|
 |
 |
-1 |
1 |
0 |
1 |
-1 |
 |
 |
|
 |
 |
-1 |
1 |
0 |
1 |
0 |
1 |
-1 |
 |
 |
 |
-1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
-1 |
 |
 |
 |
-1 |
1 |
0 |
1 |
0 |
1 |
-1 |
 |
 |
|
 |
 |
-1 |
1 |
0 |
1 |
-1 |
 |
 |
|
|
|
 |
 |
-1 |
1 |
-1 |
 |
 |
|
|
|
|
|
 |
 |
-1 |
 |
 |
|
|
|
|
|
|
|
 |
 |
 |
|
|
|
|
|
This resource count provides a constraint on board positions that
can appear in any single vacancy to single survivor problem.
One can show that for any single vacancy to single survivor problem on this
board,
after the first move and before the last move,
this resource count must always evaluate to zero.
This is a powerful constraint on the jumps available from
any board position (that can lead to a solution).
No solution can contain a jump over a peg in a hole marked "1"
(white squares) unless that jump starts at the edge of the board.
This constraint can be added to a computer program, and with it
this board is not much harder to find minimal solutions
(on a computer) than the 33-hole English board.
The above resource constraint can be applied
on the French board (by ignoring any value that is not on that board)
and it is still somewhat useful.
It can also be used on the English board,
but with only a very minor speed increase.
On Wiegleb's board a moderately useful resource count (for computations)
has a "-1" at the eight corners and "+1" at the
12 interior locations:
d2, f2, b4, d4, f4, h4, b6, d6, f6, h6, d8 and f8 (and zeros everywhere else),
see a diagram here.
How Hard Is Peg Solitaire?
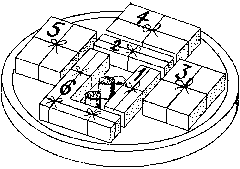
|
"Culture", a vertically oriented board with
hanging pegs
© 2013 John Robinson
|
Most people will agree that solving the central game
on the standard 33-hole board is challenging.
Long ago I spent a weekend on this puzzle without success.
However, I claim this just indicates approaching the problem by trial and error
(or exhaustive search) is very inefficient.
After you learn block removals (see [W2]),
the problem actually becomes quite simple.
It also seems that on any "well behaved" board, no matter how large, the
complement problem
should be relatively easy to solve using block removal methods.
An example of a well behaved board is any square board, but I believe
many other boards also fall into this category.
Consider a rather arbitrary board without any interior holes
(gapless).
This board might be quite large, and in the simplest case could be square.
We will try to quantify the difficulty of three different problems:
- Given an arbitrary pattern of pegs, determine if it
can be reduced to a single peg. In this case the specific shape of the board
is not important, we could even consider the board to be infinite.
- Given a complement problem on this board,
find any solution to it.
Here the shape of the board is very important.
The central game on the 33-hole board is an example of such a problem.
- Given a complement problem on this board,
find the shortest solution to it (minimum number of moves).
It was shown in 1990 [P1] that problem #1 is
NP-Complete.
In practical terms this means that any algorithm to solve this problem will
have a run
time that increases exponentially with the board size
(for example on an n by n square board).
Like problem #1, problem #2 also asks if you can
reduce a pattern of pegs to a single peg.
Does this mean problem #2 is NP-Complete also?
No, it does not, because a complement problem does not
start from an arbitrary pattern of pegs.
The starting position has every hole occupied, except for the
starting vacancy, hence it is a very regular pattern.
Clearly if the board is not null-class,
there is no solution to problem #2 or #3 (we can also check in problem #1
if the configuration of pegs is in the position class of one peg or not).
It is very easy to check if a board is null-class, so we don't need to require
this.
As the difficult case we may as well assume all boards from now on
are null-class.
Suppose we consider problem #2 on an arbitrary
rectangular
null-class board (with both edges at least 4).
Finding a solution to a complement problem on such a board, I claim,
is actually very easy, and can probably be solved in linear time.
Why? Because this problem is easy to solve by hand using block removals.
You simply visually identify blocks of pegs
you need to remove and make sure the required catalyst is present and that
after the
block removal you don't strand any pegs too far away from the core bunch.
You also need to be careful near the edge of the board.
This logic could be programmed, and would result in a computer algorithm
that could solve complement problems on rectangular boards
extremely quickly.
Even boards which are "not too different" from a rectangular board should also
be easy.
It is rather difficult to quantify "not too different", but basically any
gapless
null-class board that doesn't have any tight spaces can be solved using block
removals.
The standard 33-hole board should fit into this category.
It easier to complete this argument on
triangular boards,
and I now have a
simple algorithm
that can solve any single vacancy problem on a triangular board
of arbitrary size.
In summary, problem #1 has been proven NP-Complete.
I believe problem #2 is not very hard on "well behaved" boards,
which include at least rectangular boards (and certainly triangular boards).
Problem #3 is very difficult on
any board with more than about 50 holes, and I believe no algorithm can find
shortest solutions in polynomial time.
In 2012, Joseph Barker and Richard Korf wrote a paper on the subject
of searching for short solutions [P8].
Peg Solitaire References
See also
triangular peg solitaire references.
Books

| B1. | |
John D. Beasley,
The Ins & Outs of Peg Solitaire,
Oxford Univ. Press, 1985
(the paperback Edition 1992, contains an additional page: Recent Developments)
ISBN 0-19-286145-X (paperback).
|
| B2. | |
Martin Gardner,
The Unexpected Hanging and Other Mathematical Diversions,
University Of Chicago Press, 1991 (paperback), pp. 122-135
ISBN 0-22-628256-2.
[The chapter "Peg Solitaire" is based on a
Scientific American column that appeared in the June, 1962 edition.]
Recently updated with republished as
Martin Gardner,
Knots and Borromean Rings, Rep-Tiles, and Eight Queens,
Cambridge University Press, 2014, ISBN 0521758710.
|
| B3. | |
John H. Conway, Elwyn R. Berlekamp, Richard K. Guy,
Winning Ways for Your Mathematical Plays, Volume 4,
AK Peters, 2004 (second edition), Chapter 23, "Purging Pegs Properly".
|
| B4. | |
Walter Koetke,
Classic Thinking Games with Java,
Basics & Beyond, Inc., 2007.
|
| B5. | |
George I. Bell, Peg Solitaire with Diagonal Jumps, in
Ed Pegg Jr., Alan H. Schoen, Tom Rodgers (Editors)
Mathematical Wizardry for a Gardner,
AK Peters, 2009.
|
| B6. | |
George I. Bell, A Compendium of Peg Solitaire related papers, 2014
(175 pages, 90 pages double sided).
This is a compilation of 13 papers relating to peg solitaire (2003-2014).
You can download all the papers separately, but this makes a nice, color-coded, bound volume.
To see the list of papers, download the
Table of Contents.
Please
email me
if you would like a zip file containing all 13 papers (2.6 MB).
|
Papers
| P1. | |
Ryuhei Uehara and Shigeki Iwata,
Generalized Hi-Q is NP-complete,
Trans. IEICE, E73, pp.270-273, 1990
|
| P2. | |
George I. Bell and John D. Beasley,
New Problems on Old Solitaire Boards,
Board Game Studies #8,
presented for the 8th international colloquium on board game studies,
Oxford, England in April 2005 (finally published in
Board Game Studies Online in 2014).
|
| P3. | |
George I. Bell,
A Fresh Look at Peg Solitaire,
Mathematics Magazine, 80:16-28, 2007.
|
| P4. | |
George I. Bell,
Diagonal Peg Solitaire,
INTEGERS Electronic Journal of Combinatorial Number Theory,
Vol 7, G1, 2007.
|
| P5. | |
G. DuPuy, D. Taylor,
Using Board Puzzles to Teach Operations Research,
INFORMS Transactions on Education,
Volume 7, Number 2, January 2007.
|
| P6. | |
George I. Bell,
Notes on solving and playing peg solitaire on a computer,
last updated 2014.
|
| P7. | |
Robert A. Beeler and D. Paul Hoilman,
Peg Solitaire on Graphs,
Discrete Math. 311: 2198-2202, 2011.
|
| P8. | |
Joseph K. Barker and Richard E. Korf,
Solving Peg Solitaire using Bidirectional BFIDA*, in the
Proceedings of the Twenty-Sixth AAAI Conference on Artificial Intelligence, Toronto, 2012.
|
| P9. | |
John Beasley,
On 33-hole solitaire positions with rotational symmetry,
unpublished manuscript, 2012.
|
| P10. | |
John Beasley,
An update to the history of peg solitaire,
2014 (paper based on a presentation at the 34th International Puzzle Party in London,
UK on August 8th, 2014).
|
Web References
| W1. | |
Solitaire (pdf version),
Issue #28 (web version)
of
The Games and Puzzles Journal,
September 2003.
|
| W2. | |
Cut The Knot
contains a good description of how to solve peg
solitaire problems using block removals
(called packages and purges, Conway's terminology).
|
| W3. | |
Jurgen Koller's Peg Solitaire web site
even has ideas on how to construct your own board.
|
| W4. | |
MathWorld
has a summary page with many printed references.
|
| W5. | |
JC Meyrignac's web site
contains results from computer runs on the French Board, as well
as a peg solitaire competition and other items.
|
| W6. | |
Torsten Sillke
has
independently come up with Generalized Cross Boards.
|
| W7. | |
Sidney Cadot published an article (in Dutch) in the January 1998 issue of Machazine.
In this article he describes how he was able to calculate all
18-move solutions to the central game on the 33-hole board.
He determined that there are exactly 936 18-move solutions.
|
| W8. | |
Emmanuel Harang
has a very extensive web page on the theory of the game.
Unfortunately (for me) it is in French.
|
| W9. | |
Durango Bill
has a page on peg solitaire where he also calculates the number 23,475,688.
This is the total number of board positions reachable from the central vacancy
on the standard 33-hole board (not including positions equivalent by symmetry).
He also calculates the total number of solutions to the central game.
|
| W10. | |
Gary Darby
has created a
Delphi
program to solve peg solitaire problems,
as well as an extensive site on other mathematical games.
|
| W11. | |
The University of Waterloo has a
games museum
which contains some
interesting history on peg solitaire.
|
| W12. | |
Michel Schellekens is an Associate Professor at the National University of Ireland with an
interest in peg solitaire. (http://www.cs.ucc.ie/~mpcs/ link broken as of 2015)
|
| W13. | |
James Dalgety
has one of the largest puzzle collections in the world.
He runs puzzlemuseum.com, there you will find
history and photos of his extensive solitaire collection.
|
| W14. | |
Erich Friedman
has a
nice collection of peg solitaire puzzles.
|
| W15. | |
John Robinson (1935-2007)
was an artist who in 1993 made a
sculpture of the tree of knowledge
in the form of a peg solitaire board, with pegs representing forbidden fruit.
|
| W16. | |
This site
has some interesting ideas about the
French board.
|
| W17. | |
Rob Stegmann
has a vast puzzle web site with a nice page on
Peg Solitaire and Jumping Puzzles.
|
| W18. | |
The John and Sue Beasley Website
has some interesting recent observations of the game.
This includes a transcription from the French magazine
Mercure Galant from 1697,
where the game is described in detail.
This French article is the earliest known printed reference to peg solitaire.
|
| W19. | |
Top Accolades has a web page
which descibes the shortest solution to the central game in a way that is easy to remember.
|
| W20. | |
Jaap Scherphuis has a
peg solitaire web page,
with a nice discussion on block removals and
how to determine which problems are solvable on various boards.
Jaap also has a
Peg Solitaire Java Applet.
|
| W21. | |
A wikihow page
describing how to solve the central game
on the English board.
|
| W22. | |
The Jerry Slocum Mechanical Puzzle Collection
is one of the largest puzzle collections in the world,
and includes many rare and unusual
peg solitaire boards.
|
Copyright © 2006–2016 by George I. Bell
 To triangular lattice peg solitaire
To triangular lattice peg solitaire
 To the peg solitaire army
To the peg solitaire army
 Home
Home









 A jump is by definition a single jump of one peg over another.
When the same peg jumps one or more pegs, we call this one move.
The following terminology is useful in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep
(clearly, this terminology is only useful when n > 1).
A sweep that begins and ends at the same board location
is called a loop (or an n-loop).
A jump is by definition a single jump of one peg over another.
When the same peg jumps one or more pegs, we call this one move.
The following terminology is useful in referring to moves involving multiple
jumps: when a peg removes n pegs in a single move, we refer to it
as a sweep, or more specifically, an n-sweep
(clearly, this terminology is only useful when n > 1).
A sweep that begins and ends at the same board location
is called a loop (or an n-loop).
 For example, suppose we want to solve the puzzle mentioned above on
For example, suppose we want to solve the puzzle mentioned above on



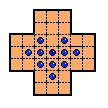
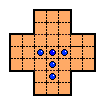

 This 36-hole board is the smallest square board on which a
complement problem is solvable.
It is the second smallest
square-symmetric, gapless board on which every
complement problem is solvable
(see [P3]).
In general it is less interesting than the English board, because
it lacks a central hole and has a simpler geometry.
It does, however, support some remarkably short solutions.
John W. Harris and Harry O. Davis studied this board in the 1960's, and found that most
single vacancy to single survivor problems can be solved in
15 moves,
with a few cases requiring 16 moves [W1].
This 36-hole board is the smallest square board on which a
complement problem is solvable.
It is the second smallest
square-symmetric, gapless board on which every
complement problem is solvable
(see [P3]).
In general it is less interesting than the English board, because
it lacks a central hole and has a simpler geometry.
It does, however, support some remarkably short solutions.
John W. Harris and Harry O. Davis studied this board in the 1960's, and found that most
single vacancy to single survivor problems can be solved in
15 moves,
with a few cases requiring 16 moves [W1].

 This was the first peg solitaire board, appearing in France in the late 17th century.
In Winning Ways For Your Mathematical Plays [B3]
it is referred to as the "Continental Board".
Antique French boards are usually paddle-shaped with a handle,
as shown on the right (see also the
board in the 1697 engraving).
Traditionally, the pegs are ivory, but have a tendency to become lost.
This was the first peg solitaire board, appearing in France in the late 17th century.
In Winning Ways For Your Mathematical Plays [B3]
it is referred to as the "Continental Board".
Antique French boards are usually paddle-shaped with a handle,
as shown on the right (see also the
board in the 1697 engraving).
Traditionally, the pegs are ivory, but have a tendency to become lost.
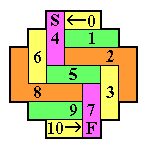
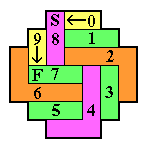
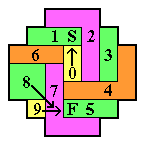
 This board, sometimes called the "Continental" Board [B3],
can be traced back to
Édouard Lucas in 1882
[B1].
This is not a null-class board, and there are only
four single vacancy to single survivor problems
solvable on it (as shown in [B1]).
This board is very difficult to play on because it has 16
corners,
but for a computer solver this is a significant constraint on play.
All four single vacancy to single survivor problems on this board
can be solved in 26 moves, but no fewer [P2].
To view solutions, see the
solution catalog.
There exist
26 move solutions with a 9-sweep,
which is rather remarkable given
all the corners on this board.
This board is not easy to decompose into block removals.
In his book, Beasley
[B1] shows how to accomplish the task using more
complex block removals to deal with all the corners.
This board, sometimes called the "Continental" Board [B3],
can be traced back to
Édouard Lucas in 1882
[B1].
This is not a null-class board, and there are only
four single vacancy to single survivor problems
solvable on it (as shown in [B1]).
This board is very difficult to play on because it has 16
corners,
but for a computer solver this is a significant constraint on play.
All four single vacancy to single survivor problems on this board
can be solved in 26 moves, but no fewer [P2].
To view solutions, see the
solution catalog.
There exist
26 move solutions with a 9-sweep,
which is rather remarkable given
all the corners on this board.
This board is not easy to decompose into block removals.
In his book, Beasley
[B1] shows how to accomplish the task using more
complex block removals to deal with all the corners.
 You can try to find a center to center solution using the
Cremers' Key
You can try to find a center to center solution using the
Cremers' Key  Several interesting variations to the 41-Hole Diamond Board have been proposed.
Around 1882, H.-A.-H. Hermary proposed removing the leftmost and rightmost holes
from the board, giving Hermary's 39-Hole board, shown on the right.
This board is
Several interesting variations to the 41-Hole Diamond Board have been proposed.
Around 1882, H.-A.-H. Hermary proposed removing the leftmost and rightmost holes
from the board, giving Hermary's 39-Hole board, shown on the right.
This board is 
 This board is null-class and
rectangular-symmetric.
It is a draughtsboard created from an 8x8 square
board,
and a convenient way to play this board is using a checkers board,
playing only on the squares of one color with diagonal jumps.
In fact this board is identical to a standard checkers board,
just rotated 45 degrees, as the figure on the right shows.
This board is null-class and
rectangular-symmetric.
It is a draughtsboard created from an 8x8 square
board,
and a convenient way to play this board is using a checkers board,
playing only on the squares of one color with diagonal jumps.
In fact this board is identical to a standard checkers board,
just rotated 45 degrees, as the figure on the right shows.





 Trying to solve the (4,0) or e1-complement problem is several orders of magnitude
harder than any problem on the
Trying to solve the (4,0) or e1-complement problem is several orders of magnitude
harder than any problem on the 
 This board is not null-class, but may be conveniently
played on a checkers or chess board using 63 coins or poker chips.
You may begin with one peg missing at any of the locations marked on the left by an X
and (potentially) finish with one peg.
From any other start (for example, anywhere along the main diagonals)
a single peg finish is impossible.
This board is not null-class, but may be conveniently
played on a checkers or chess board using 63 coins or poker chips.
You may begin with one peg missing at any of the locations marked on the left by an X
and (potentially) finish with one peg.
From any other start (for example, anywhere along the main diagonals)
a single peg finish is impossible.
 In 1986, John Harris found a
In 1986, John Harris found a
 This board is null-class,
and all SVSS problems
are easy to solve using block removal methods.
The only physical board where it is possible to play 9x9 peg solitaire is a
Go board,
I recommend using a computer board [W20].
The 9x9 board supports some remarkably long sweeps, examples are shown to the left.
A sweep of 34 is the longest geometrically possible,
shown on the red board.
What is more remarkable is that this particular sweep
can be reached from a single vacancy start.
The other sweeps shown on the left are symmetrical 32-loops.
This board is null-class,
and all SVSS problems
are easy to solve using block removal methods.
The only physical board where it is possible to play 9x9 peg solitaire is a
Go board,
I recommend using a computer board [W20].
The 9x9 board supports some remarkably long sweeps, examples are shown to the left.
A sweep of 34 is the longest geometrically possible,
shown on the red board.
What is more remarkable is that this particular sweep
can be reached from a single vacancy start.
The other sweeps shown on the left are symmetrical 32-loops.