 |
 |
 |
 |
 |
![]()
The paper in which F. A. P.
Barnard published the first perfect (what we now call Nasik) magic cubes
actually consisted mostly of material on magic squares [1].
J. R. Hendricks (Canada 1929-2007) is considered the originator of the Inlaid
Magic Square, but here are two that appeared in Barnard’s paper.
| Barnard
uses the terms bordered and inlaid and clearly defines the difference
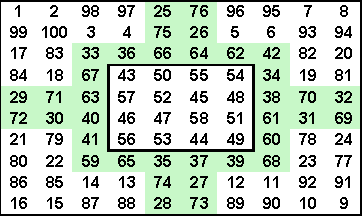
between the two types of magic squares. If you remove the green cells of this order-10 simple magic square and close up the spaces, you end up with an order-8 magic square. In both cases, the central order-4 square is pandiagonal magic. Remove the rose colored cells from this order-14 magic square and close up the array to obtain an order12 magic square. If the 5 green 4x4 squares are then removed, you obtain an order-8 magic square. Now remove all cells except those within the four 2x2 blue borders, and close up this array to obtain an order-4 pandiagonal magic square. Finally, combine all the original 2x2 bordered arrays from the original order-14 square to obtain an order-6 magic square. The squares resulting from the changes in these two squares may be seen here. Some of John Hendricks inlaid magic squares may be seen here. [1] F. A. P. Barnard, Theory of Magic Squares and Cubes, Nat. Academy of Sciences, Vol. IV, Sixth Memoir, 1888, pp 207-270 |
|
![]()
David M. Collison (U.S.A. 1933-1991) investigated generalized parts, from which he constructed what he called patchwork magic squares. [1]
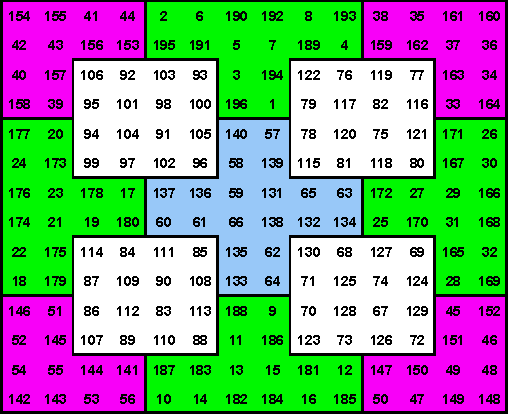
| Here I show an order-14 magic square. He
constructed it from four 4 x 4 elbows, four 6 x 4 tees, one 6 x 6 cross, and
four 4 x 4 squares. His square used associated order-4 magic squares which I
transposed in this figure, to pandiagonal magic, by moving two bottom rows
to the top, and then two left columns to the right. All figures sum to a constant in proportion to the number of cells in a line. S 14 = 1379 so S2 = 197, S4 = 394, and S6 = 591. Because all figures are magic, they can be re-arranged, using rotations and reflections to produce a large variety of different order-14 magic squares.
[1] John R. Hendricks, The Magic Square Course, self-published, 1991, 554 pages (pp 309-318)
|
 |
|
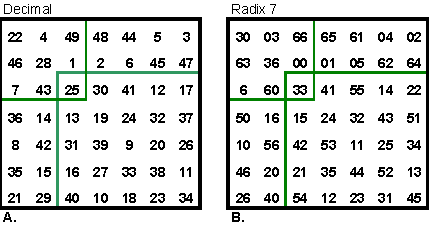
Another patchwork square by Collison is this order-7 overlapping square shown in Decimal and Radix-7 form. The Decimal normal, simple magic square with S = 175 contains an order-3 semi-magic square with S = 75, two 2 x 4 magic rectangles with S = 50 and 100, and an order-5 pandiagonal magic square with S = 125. The Radix-7 square is the
equivalent of the above, but numbered from 00 to 66 (instead of 01 to 100).
S = 330. The 3 x 3 semi-magic square contains all 2-digit combinations of
0, 3, and 6. S = 132. The two 2 x 4 rectangles have S = 66 and 165. |
 |
Gnomon: the remainder of a parallelogram after the removal of a similar parallelogram containing one of its corners.-Merriam-Webster Online
A 3 x 3
array may be dissected into a 2 x 2 array and a 5 cell gnomon in 4 ways.
When the sum of the cells in the four 2 x 2 arrays sum to the same value, the
large array is said to be a gnomon-magic square. [1]
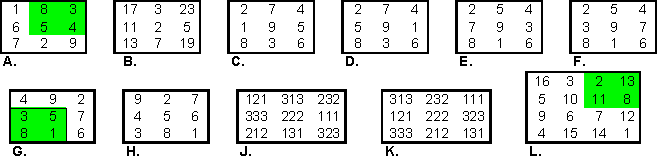
A.
is such a square. Each of the corner 2x2 regions sum to 20. Refer to these
regions as C.
B.
This gnomon square consists of the 9 smallest prime numbers. C = 33.
It is possible to
construct an infinite variety of other prime magic gnomon squares with 2 in the
center cell.
The smallest prime number C of any gnomon square with 9 distinct primes has C =
43. Can you construct it?
C.D.E.F.
Here are four gnomon-antimagic
squares. The four C's (of each) = 19, 21, 23, and 25.
G.
The Lho-shu has a
special significance in ancient Arab culture when it is considered in this
psuedo-gnomon manner [2].
The Muslim alchemist, Jabir ibn Hayyan, considered the entire material world
based on 17.
He noted too, the
series 1:3:5:8 formed the foundation for all other numbers.
28 is the typical
moon number. It is also the number of letters in the Arabic (abjad) alphabet.
The 2x2 shown in
green = 17, the gnomon = 28.
H.
Any 3x3 magic
square may be converted to a gnomon square by rotating the perimeter numbers 1
position. C = 20.
J.
is a magic square of palindromes, with S = 666. It is an antimagic gnomon
because the C’s = 989, 878, 898, and 787.
K. Rotating
the outer numbers results in a gnomon square with C = 888.
L.
The Durer (1514) magic
square is an example of an order-4 Gnomon-magic square because the four cells in
each quadrant sum to 34.This is true for all 432 order-4 squares of Groups I to
VI-A.
[1] Charles W. Trigg, Third Order
Gnomon-Magic Squares, Journal of Recreational Mathematics, 18:1, 1985-86, pp
25-36
Charles W. Trigg, Third Order Gnomon-Magic Squares with Distinct Primes,
Journal of Recreational Mathematics, 19:1, 1987, pp 1-2
Charles W. Trigg, A Remarkable Group of Gnomon-Antimagic Squares,
Journal of Recreational Mathematics, 19:3, 1987, pp 164-168
[2] Annemarie Schimmel, The Mystery of Numbers, Oxford University Press,1991,
0-19-508919-7
On the cover of the now defunct REC [1], Clifford Pickover posed as a puzzle, an unusual number square.
You have 25 squares in a 5x5 array. They contain 12 1s, a single 2, and the rest 0s. Rearrange the digits so the sum of each row, column, and the two main diagonals are positive and even. See a. for the puzzle and b. for Pickover’s solution.

The following issue of REC contained a number of additional solutions, including c. from Dennis Sulllivan and a similar symmetrical one (d.) from Harry J. Smith. An example of an unsymmetrical one is e., from Donn Kirk, who reported that there is at least one solution with the 2 in an given position! Dr. Robert Stong reported that this problem could be solved by starting with an order 5 magic square. First replace every odd entry with a zero, then every even entry with a one. Finally, replace one of the zeros with a two.
[1] Recreational & Educational Computing, Dr. Michael Ecker, Volume 12, Number
3 (and 4) January (and March) 1998.
(REC)
http://members.aol.com/DrMWEcker/REC.html
![]()
Imagine a magic square where each cell is a square tower equal to the height of the cell’s numerical value. Craig Knecht refers to this model as a topographical magic square. He has explored this type of magic square for the feature of how much water would be retained in the central part of the square. Topographical squares and some results of his discoveries are displayed on his new web site at http://www.knechtmagicsquare.paulscomputing.com/
|
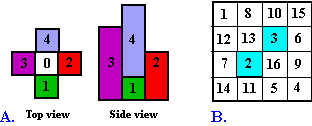
Figure A. shows top and side views of a 3 x 3 model (not magic) where water could be poured into the center cell which would retain 1 unit before pouring over the cell with height equal to 1. Of the 880 order-4 magic
squares he found that 137 would retain no water.
Craig shows topographical squares of other orders on his site. |
 |
|
On July 30, 2008, I received this more complex topographical magic square from him. C. contains a 'lake' with an 'island' in it.
On his
site Craig also demonstrates mass in regards to magic squares and some work with
paths.
He also has a page about the Formula One constraint Logic programming language.
Craig Knecht, Walter Trump, Francis Gaspalou, and Peter Loly investigated moment of inertia of magic squares.
| Wilfred
Steimel of Germany specializes in unusual magic squares. Here are two of his
non-normal magic squares in which some digits are not used. I received these
by email on May 31, 2008. a. is pandiagonal magic but contains no 0. 6, 7, 8, or 9 and so is not normal. S = 165 b. is non-normal, simple, concentric, and contains no digit 9. S for orders 3, 5, 7 and 9 are 183, 305, 427, and 549. The sum of the 9 colored cells in each of the 3 sets equals the S9 value, 549. |
|
![]()
|
Recently Christian Boyer added a new Update page to his excellent Multimagic site. Link I leave it to you to explore these new additions. Here I show two representative squares from elsewhere on his site. Since 2007, Lee
Morgenstern has constructed several orders 4, 5, and He proved that orders
3 and 4 add-multiply magic squares are impossible. Is an order 5, 6, or 7
possible? S = 360 P =
8491392000
To the right is a 6x6 magic square of cubes constructed in 2008 by Lee Morgenstern. It uses all the integers from -18 to 18 (except 0). S = 0. It is unknown if
regular magic squares of cubes are possible for orders Christian Boyer constructed the first known orders 9, 10 and 11 normal magic squares of cubes in late 2006. |
 Order-6
Add-Multiply Square Order-6
Add-Multiply Square
|
Edward Gutierrez has a
new site with the long name
ODD MAGIC SQUARES USING TEN NEW ALGORITHMS AND PARITY
THE WHEEL, LOUBÈRE AND
MÉZIRIAC METHODS
|
This site introduces two new methods used for the construction of semi-associated odd magic squares. The method consists of pairing numbers in complementary fashion, partitioning these complementary pairs into groups and placing these groups into a square in a certain order using parity as an aid. This example is taken
from his New Modified Wheel and De La Loubère Methods |
|
![]()
In one of his recent papers [1] Peter Loly [2] discusses a large variety of magic square and hypercube issues. Includes is mention of an unusual pandiagonal non-magic number square. If the decimal integers (0-15) are converted to a special binary number system called Gray code. binary, adjacent cell numbers, in both the horizontal and vertical direction change by just 1 digit. This example is one of 48 such squares out of a total of 3,465,216 order-4 pandiagonal non-magic squares.
Gray code:
Definition: An ordering of 2n binary numbers
such that only one bit changes from one entry to the next.
An n-bit Gray code corresponds to a
Hamiltonian cycle on an n-dimensional hypercube.
Hamiltonian cycle: Definition: A
path through a
graph that starts and ends at the
same vertex and includes every
other vertex exactly once.
The gray code is sometimes referred to as reflected binary, because the first eight values compare with those of the last 8 values (of regular binary), but in reverse order.
This table is presented for the convenience of those not too familiar with the binary (radix 2) number system, or with the Gray code.
|
Decimal |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
Binary |
0000 |
0001 |
0010 |
0011 |
0100 |
0101 |
0110 |
0111 |
1000 |
1001 |
1010 |
1011 |
1100 |
1101 |
1110 |
1111 |
|
Gray |
0000 |
0001 |
0011 |
0010 |
0110 |
0111 |
0101 |
0100 |
1100 |
1101 |
1111 |
1110 |
1010 |
1011 |
1001 |
1000 |
|
Decimal (Gray) |
0 |
1 |
3 |
2 |
6 |
7 |
5 |
4 |
12 |
13 |
15 |
14 |
10 |
11 |
9 |
8 |
|
The Gray code square.
The 2-digit numbers in the top row appear as
least significant digits in each column. Notice that the square is constructed simply by filling the rows in alternate directions, sequentially from the string of Gray code values. |
[1]
Peter D. Loly,
Franklin Squares: A Chapter in the Scientific Studies of Magical Squares,
Complex
Systems, 17 (2007) 143–161
[2] Some of his other papers on magic squares are at
http://home.cc.umanitoba.ca/~loly/
![]()
Has a site at http://www.gaspalou.fr/magic-squares/ with much material on the methods and tools for enumeration of magic squares.
Among other results he confirmed the total (275,305,224) for order-5 squares. This value was first determined by Richard Schroeppel in 1973, then independently confirmed by Walter Trump.
Neil Campbell has discovered a new class of anti-magic squares with features similar to the pandiagonal magic square.
A normal anti-magic square has sums for the orthogonal lines and the main diagonals that must be unique and consecutive. (if the sums are not consecutive, the figure is a heterosquare.)
By changing the above definition slightly, it is possible to construct a square with the above features plus all the broken diagonals also summing correctly. This means that the square can then by transformed to another pandiagonal (nasik) anti-magic square by moving a line from one side to the opposite side.
|
The
slight change in the definition is: The order-4 example has 32 sums in consecutive order. Sums range from 14 to 46 skipping the magic constant 30 I have a page on anti-magic and heteromagic squares here. |
|
Neil's father Dwane has a web site that discusses Nasik (Perfect) magic hypercubes and has some hypercube generator programs available for downloading. He discusses at some length, theory of construction and methods of testing nasik hypercubes. His site is at http://home.earthlink.net/~dwanecampbel/.
![]()
Pandiagonal magic squares
have also been called perfect. But who first introduced this term?
A fairly short search uncovered some early users.
F. A. P. Barnard, on the first page of his paper says
Magic squares
are distinguished into two classes, ordinary and perfect,...'
… If the sums of the numbers in the broken diagonals, equal in every case, the
sums found in the vertical and horizontal rows, the square is perfect.
[1]
Emory McClintock, On the 2nd page of his paper Most Perfect Forms of Magic Squares, he states
By reason of these remarkable properties pandiagonal squares have received from some writers, beginning with La Hire, the name ‘perfect”, and with others, beginning with Lucas, the name “diabolic”. [2]
The term Nasik, we know, was introduced by A. H. Frost in 1866 [3] for pandiagonal magic squares and pandiagonal-like magic cubes. It was refined by C. Planck in 1905 [4][5] to cover all dimensions of hypercubes where all possible lines some correctly!
See my Nasik article for reasons why we should replace the term perfect with the term nasik!
[1] F. A. P. Barnard, Theory of Magic
Squares and Cubes, Nat. Academy of Sciences, Vol. IV, Sixth Memoir, 1888, pp
207-270
[2] Emory McClintock, On the Most Perfect Forms of Magic Squares, with
Methods for their Production, American Journal of Mathematics, 1897, 19, pp
99-120.
[3] A. H. Frost, Invention of Magic Cubes, Quarterly Journal of
Mathematics, 7, 1866, pages 92-102. See page 99, para. 23 and page 100, para.
26.
[4] C. Planck, The Theory of Path Nasiks, Printed for private circulation
by A. J. Lawrence, Printer, Rugby (England),1905 (Available from The University
Library, Cambridge).
[5] W. S. Andrews, Magic Squares and Cubes. Open Court Publ.,1917.
Pages 365,366, by Dr. C. Planck.
Re-published by Dover Publ., 1960 (no ISBN); Dover Publ., 2000, 0486206580;
Cosimo Classics, Inc., 2004, 1596050373
Please send me Feedback about my Web
site!![]()
![]()

![]()
Harvey Heinz harveyheinz@shaw.ca
This page originally posted in August 2008
This page last updated
September 21, 2009
Copyright © 2008 by Harvey D. Heinz