 |
 |
 |
 |
 |
![]()
Introduction |
A brief description of how 36 makes 144 makes 3600
pandiagonal magic squares. |
Transforming 36 to 144 |
Change rows & columns in order 1-3-5-2-4, then diagonals
to rows and . finally each of these four squares to 25 by cyclical permutation of rows and columns. |
List of 36 Essentially different |
The 36 essentially different order-5 pandiagonal magic
squares and relationship to Grogono's and Suzuki's lists of 144 'unique' or 'fundamental'
squares. |
It gets better! |
You can construct all 3600 order-5 pandiagonal magic squares
from just 1 square. |
Cyclical (regular) pandiagonal magic squares |
A summary and a comparison with orders 3, 7 and 11 |
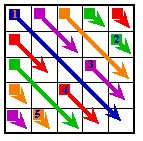
There are 36 ‘essentially different’ order-5 pandiagonal magic squares that can each be transformed into 3 other magic squares. The resulting 144 pandiagonal magic squares can each in turn be transformed cyclically to 24 other magic squares by successively moving a row or column from 1 side of the square to the other side. Completing these transformations on all 36 essentially different magic squares will produce the complete set of 3600 pandiagonal magic squares of order-5.
Each of the 36 essentially different magic squares is transformed to 3 others as follows.
The total number of order-5 pandiagonal basic magic squares is 36 times 4 times 25 equals 3600.
![]()
 |
|
Transform # 1 by 1-3-5-2-4
|
and then columns
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Convert original diagonals | Square # 1 (original | # 1 change order of rows | to square # 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
From above square to # 2
|
The 4 basic transformations An example of how four squares are obtainable from each 'essentially different' order-5 pandiagonal magic square. |
From above square to # 4
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| To new rows | diagonals to rows | diagonals to rows |
![]()
An essentially different order-5 magic square is defined as follows ( Benson & Jacoby).
All references to the number of magic squares refers to the basic squares which is normally understood in magic square discussions. Alan Grogono, in contrast, uses the mathematical approach and considers the total number of squares (which includes rotations and reflections).
![]()
When making the above transformations, the resulting magic square will not necessarily be normalized. That is, the second cell in the top row may not be smaller then the first cell in the second row. If required, this may simply be done by reflecting the square around the leading diagonal (exchanging rows and columns). No rotation will be required because the top left hand cell will always contain the number 1.It seems that if the original square is basic, about 4 of the 24 squares resulting from the cyclical transformation will be basic and the other 20 will require normalizing. If the original square is not basic, none of the other 24 will be either.
A comparison of the following derivatives from square # 31 with those above from square
# 1 will show that different squares require normalization to produce a basic magic
square.
Notice that the 36 essentially different squares I show on this page match the first of
the 144 squares shown by Grogono and Suzuki (although all 3 sets are listed in different
orders.
However, only 1 of the 6 squares derived from #1 and #31 (shown above) match a square in
Grogono’s list of 144 and none of the 6 match any of Suzuki’s 144.
Original # 31 |
# 31 transformed |
# 31 to 1-3-5-2-4 |
Square to left to |
|||||||||||||||||||
1 |
7 |
24 |
18 |
15 |
1 |
13 |
17 |
25 |
9 |
1 |
24 |
15 |
7 |
18 |
1 |
17 |
9 |
13 |
25 |
|||
19 |
13 |
5 |
6 |
22 |
22 |
10 |
4 |
11 |
18 |
10 |
17 |
3 |
21 |
14 |
14 |
23 |
5 |
16 |
7 |
|||
10 |
21 |
17 |
14 |
3 |
14 |
16 |
23 |
7 |
5 |
23 |
11 |
9 |
10 |
2 |
20 |
6 |
12 |
24 |
3 |
|||
12 |
4 |
8 |
25 |
16 |
8 |
2 |
15 |
19 |
21 |
19 |
5 |
22 |
13 |
6 |
22 |
4 |
18 |
10 |
11 |
|||
23 |
20 |
11 |
2 |
9 |
20 |
24 |
6 |
3 |
12 |
12 |
8 |
16 |
4 |
25 |
8 |
15 |
21 |
2 |
19 |
|||
1 ,3, 5, 2, 4 to => |
Diagonals to rows |
rows and columns |
Diagonals to rows |
|||||||||||||||||||
When the cyclical permutations are performed, again many squares will require normalization.
Because different lists of the 144 fundamental magic squares may be compiled differently, lists by different persons will very likely not match.
Regardless of which list of the 144 fundamental squares is used, after the cyclical permutations are performed, and all resulting squares are normalized (where required), the resulting list of sorted 3600 pandiagonal magic squares will be identical. This suggests that an intermediate normalization step may be dispensed with, and only the final normalization be performed, where required, on the finished list.
Alan Grogono refers to these 144 squares as ‘unique’. (He uses the number series from 0 to 24 instead of 1 to 25 to simplify mathematical computing.) http://www.grogono.com/magic/text-5x5pan144.shtml#Subtop
Mutsumi Suzuki refers to them as "fundamental’. His pages are now found in the MathForum
The following 36 essentially different magic squares were compiled from tables in
W. H. Benson and O. Jacoby, New Recreations With Magic Squares, Dover, 1976,
0-486-23236-0
The left hand number above each square is the Benson & Jacoby sequence number.
The middle number is the number in Grogono’s list of 144 unique magic squares.
The right hand number is the number of the square in Suzuki’s list of 144 fundamental
magic squares.
1 2 35 2 4 31 3 1 24 4 3 20 5 6 33 6 8 27 1 7 13 19 25 1 7 13 20 24 1 7 13 24 20 1 7 13 25 19 1 7 14 18 25 1 7 14 20 23 14 20 21 2 8 15 19 21 2 8 14 25 16 2 8 15 24 16 2 8 13 20 21 2 9 15 18 21 2 9 22 3 9 15 16 22 3 10 14 16 17 3 9 15 21 17 3 10 14 21 22 4 8 15 16 22 4 10 13 16 10 11 17 23 4 9 11 17 23 5 10 11 22 18 4 9 11 22 18 5 10 11 17 24 3 8 11 17 24 5 18 24 5 6 12 18 25 4 6 12 23 19 5 6 12 23 20 4 6 12 19 23 5 6 12 19 25 3 6 12 7 5 22 8 7 16 9 10 29 10 12 25 11 9 18 12 11 14 1 7 14 23 20 1 7 14 25 18 1 7 15 18 24 1 7 15 19 23 1 7 15 23 19 1 7 15 24 18 13 25 16 2 9 15 23 16 2 9 13 19 21 2 10 14 18 21 2 10 13 24 16 2 10 14 23 16 2 10 17 4 8 15 21 17 4 10 13 21 22 5 8 14 16 22 5 9 13 16 17 5 8 14 21 17 5 9 13 21 10 11 22 19 3 8 11 22 19 5 9 11 17 25 3 8 11 17 25 4 9 11 22 20 3 8 11 22 20 4 24 18 5 6 12 24 20 3 6 12 20 23 4 6 12 20 24 3 6 12 25 18 4 6 12 25 19 3 6 12 13 14 34 14 13 30 15 15 12 16 16 8 17 18 36 18 17 26 1 7 18 14 25 1 7 18 15 24 1 7 18 24 15 1 7 18 25 14 1 7 19 13 25 1 7 19 15 23 13 24 5 6 17 13 25 4 6 17 19 25 11 2 8 20 24 11 2 8 14 23 5 6 17 14 25 3 6 17 10 16 12 23 4 9 16 12 23 5 12 3 9 20 21 12 3 10 19 21 10 16 12 24 3 8 16 12 24 5 22 3 9 20 11 22 3 10 19 11 10 16 22 13 4 9 16 22 13 5 22 4 8 20 11 22 4 10 18 11 19 15 21 2 8 20 14 21 2 8 23 14 5 6 17 23 15 4 6 17 18 15 21 2 9 20 13 21 2 9 19 19 10 20 20 4 21 22 32 22 21 28 23 23 6 24 24 2 1 7 19 23 15 1 7 19 25 13 1 7 20 13 24 1 7 20 14 23 1 7 20 23 14 1 7 20 24 13 18 25 11 2 9 20 23 11 2 9 15 23 4 6 17 15 24 3 6 17 18 24 11 2 10 19 23 11 2 10 12 4 8 20 21 12 4 10 18 21 9 16 12 25 3 8 16 12 25 4 12 5 8 19 21 12 5 9 18 21 10 16 22 14 3 8 16 22 14 5 22 5 8 19 11 22 5 9 18 11 9 16 22 15 3 8 16 22 15 4 24 13 5 6 17 24 15 3 6 17 18 14 21 2 10 19 13 21 2 10 25 13 4 6 17 25 14 3 6 17 25 26 21 26 25 17 27 28 9 28 27 5 29 30 23 30 29 13 1 7 23 14 20 1 7 23 15 19 1 7 23 19 15 1 7 23 20 14 1 7 24 13 20 1 7 24 15 18 13 19 5 6 22 13 20 4 6 22 18 14 5 6 22 18 15 4 6 22 14 18 5 6 22 14 20 3 6 22 10 21 12 18 4 9 21 12 18 5 10 21 17 13 4 9 21 17 13 5 10 21 12 19 3 8 21 12 19 5 17 3 9 25 11 17 3 10 24 11 12 3 9 25 16 12 3 10 24 16 17 4 8 25 11 17 4 10 23 11 24 15 16 2 8 25 14 16 2 8 24 20 11 2 8 25 19 11 2 8 23 15 16 2 9 25 13 16 2 9 31 32 11 32 31 1 33 34 19 34 33 15 35 36 7 36 35 3 1 7 24 18 15 1 7 24 20 13 1 7 25 13 19 1 7 25 14 18 1 7 25 18 14 1 7 25 19 13 19 13 5 6 22 19 15 3 6 22 15 18 4 6 22 15 19 3 6 22 20 13 4 6 22 20 14 3 6 22 10 21 17 14 3 8 21 17 14 5 9 21 12 20 3 8 21 12 20 4 9 21 17 15 3 8 21 17 15 4 12 4 8 25 16 12 4 10 23 16 17 5 8 24 11 17 5 9 23 11 12 5 8 24 16 12 5 9 23 16 23 20 11 2 9 25 18 11 2 9 23 14 16 2 10 24 13 16 2 10 23 19 11 2 10 24 18 11 2 10
![]()
| We have defined what is an ‘essentially different’ pandiagonal
magic square. Each of these 36 squares (order-5) may then be transformed by the diagonal
to rows transformation, then each of these two by the 1-3-5-2-4 row and column change.
Then each of these 4 by the 25 cyclical transformations to construct 100 different basic
pandiagonal magic squares. But it gets better! All 3600 order 5 pandiagonal squares may be constructed from this one ‘intermediate’ square. |
|
||||||||||||||||||||||||||||||
Notice that in this figure, each upper case letter and each lower case letter appears once in each row, column and diagonal indicating that this is a cyclical magic square. The fact that each letter appears once in each broken diagonal indicates that it is pandiagonal.
The values for the capitol letters may be assigned the values 0, 5, 10, 15 and 20 (in any order). For the lower case letters, the values are 1, 2, 3, 4, 5, again in any order. Or the Capitol letters may represent the low numbers with the high numbers assigned to the lower case letters.
Now, there are 10 ways we can select A. It may be any one of the set of 5 high numbers or any one of the set of five low numbers. For each of these 10 ways there are 4 ways to select B (any of the four remaining numbers from the set A was chosen from. For each of these 40 ways, there are 3 ways to select C. And finally two ways to select D (and 1 way only to select E). Similarly, for each of these 240 ways, there are 5 x 4 x 3 x 2 x 1 ways to select the lower case values. This gives us a total of 240 x 120 = 28,800 = 2(5!)2. Dividing this figure by 8 gives us the 3600 basic order 5 pandiagonal magic squares.
The complete list of 3600 order-5 pandiagonal magic squares are available for download.
![]()
Here I will present a condensation of what we have been discussing and a comparison with orders 7 and 11 cyclical pandiagonal magic squares.
Order-5 pandiagonal magic squares are of a type called Cyclical or Regular. This type of magic square has each cell containing a number represented by a capitol and lower case letter, and each letter appearing once in each row and column. All orders 4 and 5 pandiagonal magic squares are of this type.
Order-7 contains 38,102,400 cyclical pandiagonal magic squares. (It contains 640,120,320 non-cyclical (irregular) pandiagonal magic squares {Prof. Albert L. Candy}.) Order-7 pandiagonal magic squares, have two possible non-cyclical transformations. Namely 1-3-5-7-2-4-6 and 1-4-7-3-6-2-5.
For a given order, n, (where n is a prime number) there are (n-3)(n-4)(n!)2/8 basic cyclical pandiagonal magic squares.
| [1] Order (n) |
[2] Total Cyclical Basic Pandiagonal |
[3] Intermediate squares |
[4] Each [3] square gives |
[5] Essentially different |
[6] Each [5] square gives |
| 3 | 0 | 0 | 0 | 0 | 0 |
| 5 | 3600 | 1 | 3600 | 36 | 100 |
| 7 | 38,102,400 | 6 | 6,350,400 | 129,600 | 294 |
| 11 | 11,153,456,455,680,000 | 28 | 398,337,730,560,000 | 921,773,260,800 | 12,100 |
| (n-3)(n-4)(n!)2/8 | (n-3)(n-4)/2 | (n!)2/4 | [2]/[6] | (n-1)(n2) |
Column [6] figures are obtained by:
Order-5 essentially different square + 1-3-5-2-4, then the diagonal to row transformation
for each of these gives 4 magic squares x the 25 cyclical transformations gives the 100
squares shown in column 6.
Order-7 is similar except there are two row/column transformations (see above). This gives
us 6 magic squares times 72 = 294 magic square for each essentially different
square.
The number of essentially different pandiagonal magic squares (column [5] is obtained by
column [2] divided by column [6].
![]()
Please send me Feedback about my Web
site!![]()

![]()

![]()
Last updated
September 01, 2009
Harvey Heinz harveyheinz@shaw.ca
Copyright © 2001 by Harvey D. Heinz