Pentacube Oddities with 4-Rotary Symmetry

Introduction

A pentacube is a solid made of five cubes joined face to face. An oddity (or Sillke Figure) is a figure with even symmetry formed by an odd number of copies of a polyform.

In 1996, Torsten Sillke reported having found a point-symmetric arrangement of 17 F pentacubes. He asked whether 17 is the least such odd number, and more generally whether an odd number of copies of a polycube can be arranged to achieve any given symmetry. This was the earliest known mention of polyform oddities.

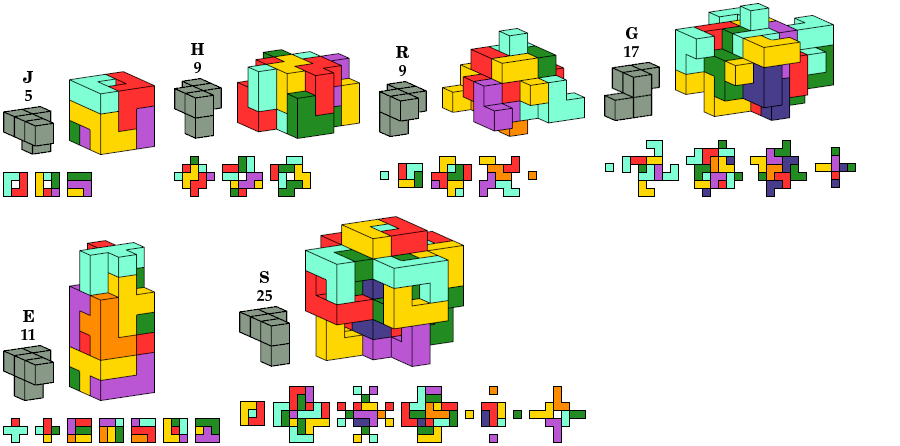
Polycubes have 33 symmetry classes (including asymmetry), and 31 of them have even order. That is too many to show here. Instead I show only oddities with 90° rotary symmetry around an orthogonal axis. In all pictures, the cross-sections are shown from top to bottom. If you find a smaller solution, please write.

Bryce Herdt improved on one of my solutions.

Thanks to Joyce Michel for suggesting improvements to this page.

For other classes of symmetry, see:

  • Pentacube Oddities with Orthogonal Mirror Symmetry
  • Pentacube Oddities with Diagonal Mirror Symmetry
  • Pentacube Oddities with Orthogonal Rotary Symmetry
  • Pentacube Oddities with Diagonal Rotary Symmetry
  • Pentacube Oddities with Inverse Symmetry
  • Pentacube Oddities with Double Orthogonal Mirror Symmetry
  • Pentacube Oddities with Double Diagonal Mirror Symmetry
  • Pentacube Oddities with Square Symmetry
  • Pentacube Oddities with Full Symmetry

    • Nomenclature

    Orthogonal 4-Rotary Symmetry

    Orthogonal 4-rotary symmetry is the symmetry of 90° rotation about an axis perpendicular to some faces of the cells.

    The smallest example of a polycube with orthogonal 4-rotary symmetry and no stronger symmetry is this dodecacube (12-cube), as found by W. F. Lunnon:

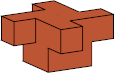
    Achiral Pentacubes

    The solutions for pentacubes I and X are trivial. Those pentacubes already have orthogonal 4-rotary symmetry.

    The solutions for pentacube V is its smallest known oddity with full (achiral cubic/octahedral) symmetry. No smaller solutions is known.

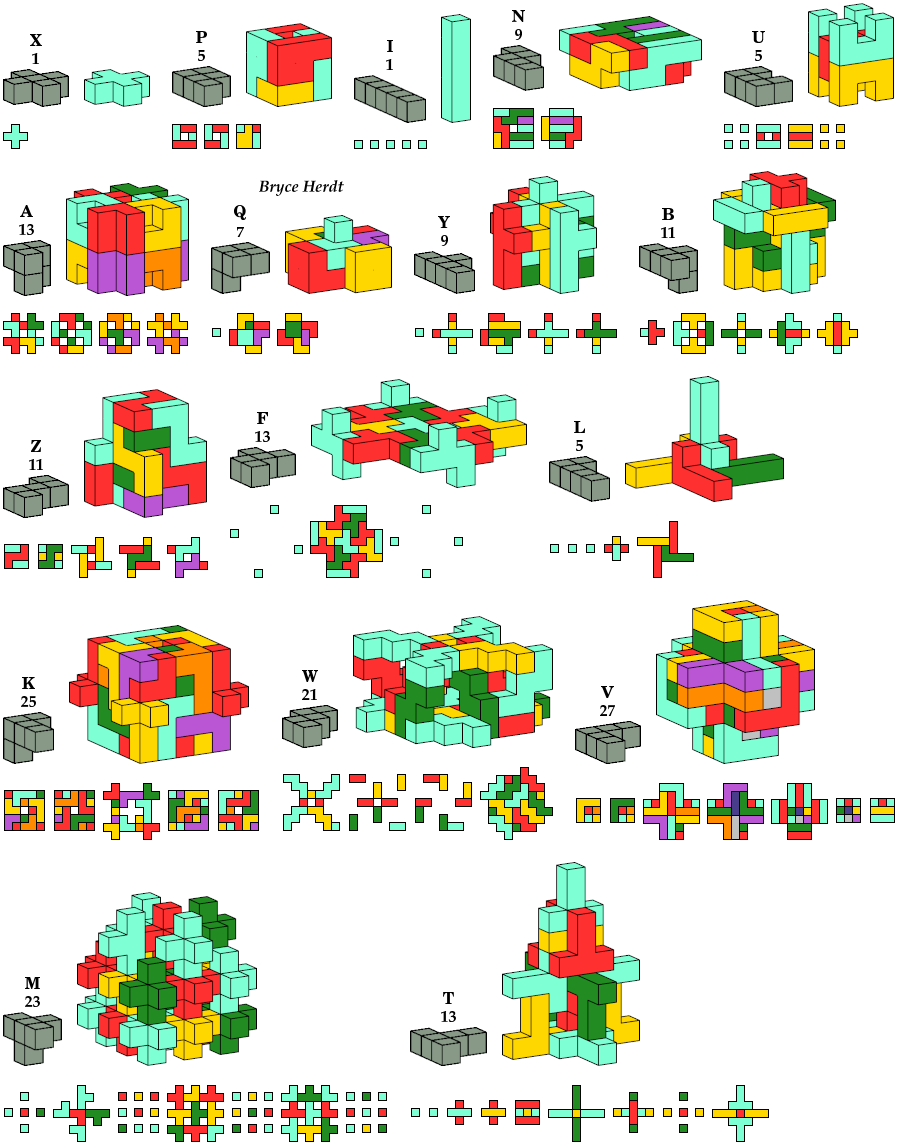
    Chiral, Disallowing Reflection

    The oddity for the S pentacube is formed by joining three minimal odd boxes. No smaller solution is known.

    Unsolved

    Chiral, Allowing Reflection

    Last revised 2024-03-23.

    Back to Polyform Oddities < Polyform Curiosities
    Col. George Sicherman [ HOME | MAIL ]