

Epistle to Richard Boyle
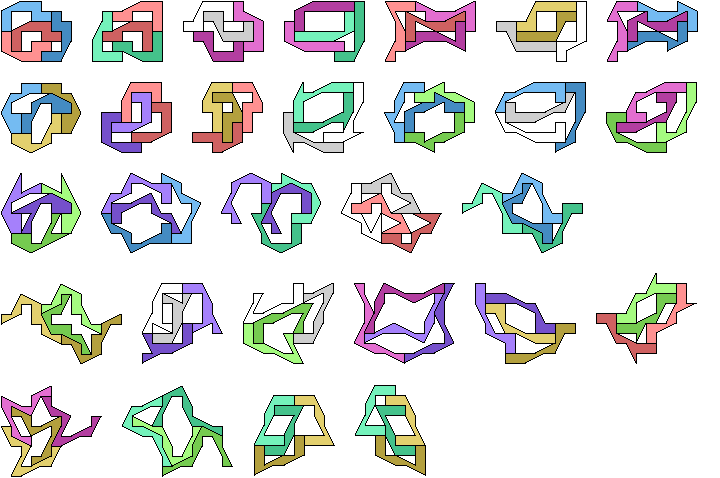
The first to study tetrads was Walter Trump, in 1970 or 1971. He recorded his findings in notebooks, but did not publish them. In 2020 he presented them on his website Further Questions About Tetrads. It contains a great deal of general and specific information about tetrads.
Michael R. W. Buckley first used the name tetrad in a 1975 article in the Journal of Recreational Mathematics, volume 8. In 1979 Trump sent many of his results to Martin Gardner, including the holeless 11-omino tetrad shown under Polyominoes and Polynars.
Martin Gardner's book Penrose Tiles to Trapdoor Ciphers (Freeman, 1989; ISBN 0-7167-1987-8) also shows some plane constructions by Scott Kim, including a holeless tetrad for a 12-omino, a holeless tetrad for a 26-iamond with mirror symmetry, and a holeless tetrad for a tetrahex. Karl Scherer shows many varieties of tetrads at Wolfram.
Here I consider only tetrads that are themselves polyforms of the same type as their tiles.
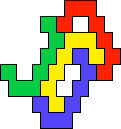
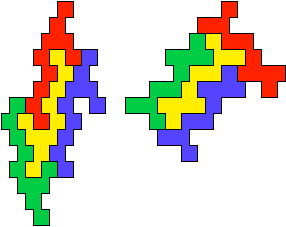
The smallest polyabolo tetrads, found by Juris Čerņenoks, use 12-aboloes:


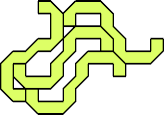
The smallest tetrad for a polyabolo with mirror symmetry uses a 26-abolo or 13-omino:
Dr. Karl Scherer found this holeless tetrad for a symmetric polyabolo. It uses a 278-abolo with only 27 edges:
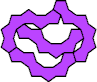

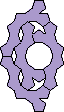
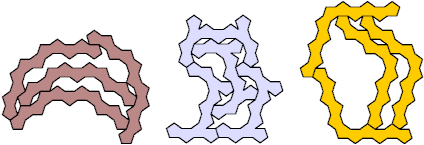
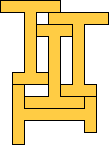
The smallest tetrad for a polypent with bilateral symmetry about an edge uses a 12-pent:
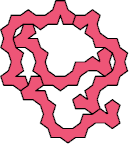
The smallest tetrad for a polypent with birotary symmetry uses a 12-pent:
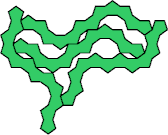

The smallest tetrad for a symmetric polyhept uses 15-hepts:
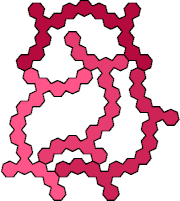
The smallest tetrads for polyhepts with mirror symmetry around an edge use 16-hepts:
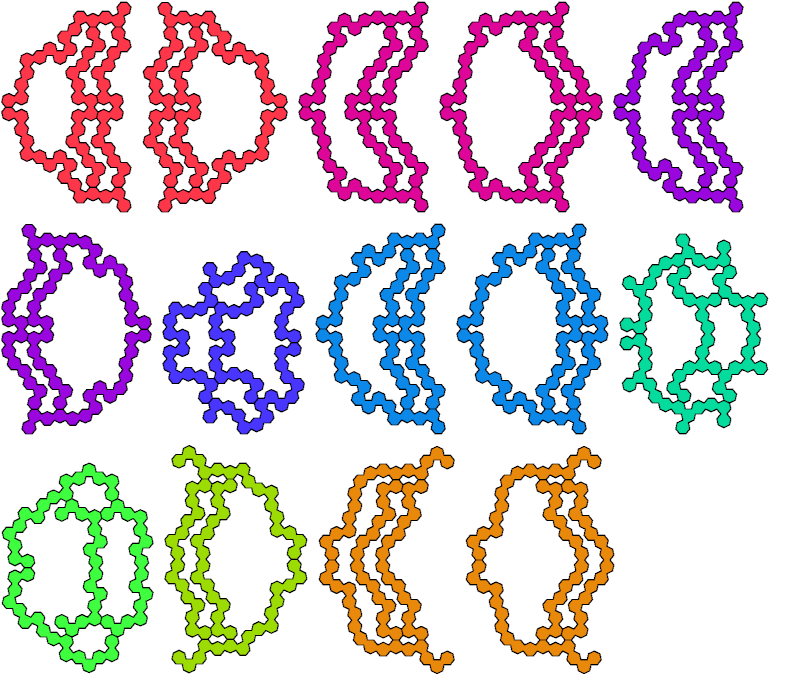
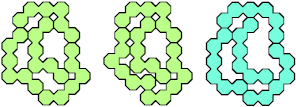
The smallest tetrads for a symmetric polyoct use 10-octs:

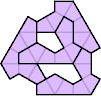
The smallest tetrads for polyocts with diagonal symmetry use 13-octs:

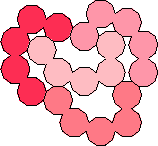
The smallest tetrads with symmetric polykites of odd order use 13-kites:
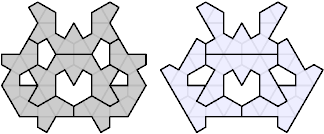
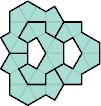
The smallest holeless tetrad with symmetric polykites uses 16-kites:
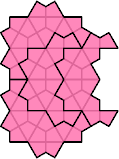
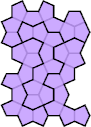
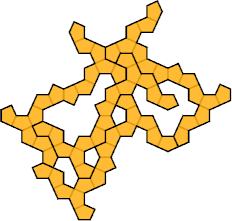
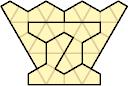
The smallest tetrad for polycairos with bilateral symmetry uses 18-cairos.
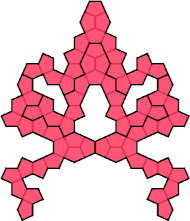
The smallest polydom tetrad uses a hexadom:
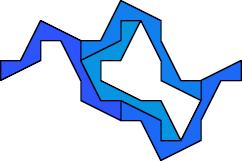
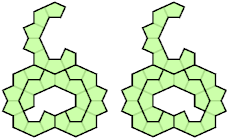
There are 28 heptadoms that can form tetrads:
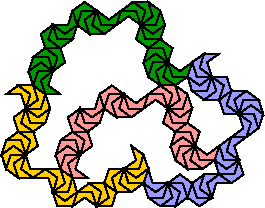
I converted the pentadec tetrad shown under Polydecs to a polycrown tetrad by tiling each decagon with 10 crowns. After that, Edo and I took turns deleting more and more superfluous crown cells.
Edo found another 29-crown tetrad, similar to that shown above, in which some cells are relocated within their enclosing decagons.
I am searching for a polycrown tetrad that is not derived from the pentadec tetrad.
So the 29-crown tetrad shown above can be converted to use a 29-gold. But this polygold tetrad is smaller:
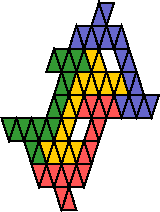
It uses an 18-gold. I made it by stretching a polyiamond tetrad in which the tile is rotated only by 180°. See Polyiamond and Polymar Tetrads.
This tetrad may not be minimal.
Around 1979 Walter Trump found the the fewest edges for a polygon that can form a tetrad:
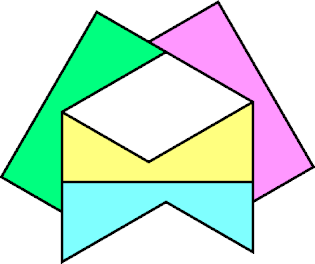
Later Livio Zucca found another pentagon solution:
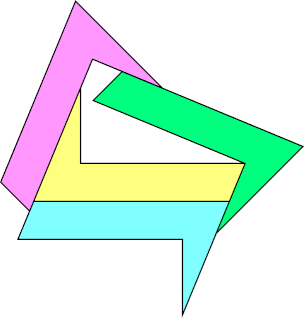
Last revised 2026-01-03.