From 1999 to 2005 Livio Zucca maintained a vast website of mathematical
recreations called Remembrance of Software Past.
It was full of new ideas, attracting contributions from
many talented mathematicians.
Unfortunately, it was hosted by GeoCities,
which was shut down in 2009.
Fortunately Giovanni Resta reconstructed Remembrance
in full on his host
Iread.it.
Deteriorating eyesight left Livio unable to maintain his site.
With Livio's permission I have revived his Remembrance
pages
about polyomino compatibility.
I have updated the links and many of the solutions.
Livio and I welcome new contributions.
If you would like to submit an improved solution, or a new solution,
or a new idea, please write me at colonel4@comcast.net.
For other pages on polyform compatibility, see Polyform Compatibility.
 | Pento-Tro-Dominoes. Find a figure that can be tiled with any of a given pentomino, tromino, and domino. |
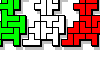 | Pento-Tetro-Trominoes. Find a figure that can be tiled with any of a given pentomino, tetromino, and tromino. |
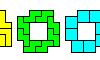 | Tetrominoes Challenge. Find a figure that can be tiled with each of a given set of tetrominoes and no others. |
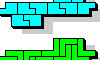 | Triple Pentominoes. Find a figure that can be tiled with each of three given pentominoes. |
 | Pentomino Odd Pairs. Find a figure that can be tiled with an odd number of either of two pentominoes. |
 | Holeless Pentomino Odd Pairs. Holeless solutions for Pentomino Odd Pairs. |
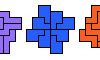 | Holeless Triple Pentominoes. Holeless solutions for Triple Pentominoes. |
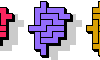 | Pentomino Odd Triples. Like Triple Pentominoes, with an odd number of tiles. |
 | Quadruple Pentominoes. Find a polyomino that can be tiled with each of four different pentominoes. |
 | Pentabolo Odd Pairs. Given two pentaboloes, Given two pentahexes, construct a figure that can be tiled with either using an odd number of tiles. |
 | Pentahex Odd Pairs. Given two pentahexes, construct a figure that can be tiled with either using an odd number of tiles. |
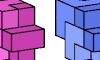 | Pentacube Odd Pairs. Given two pentacubes, construct a figure that can be tiled with either using an odd number of tiles. |
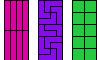 | Pento-Tetro-Tetrominoes. Given a pentomino and two tetrominoes, find a polyomino that each can tile. |
 | Pento-Pento-Tetrominoes. Given two pentominoes and a tetromino, find a polyomino that each can tile. |
 | Triple Hexiamonds. Given three hexiamonds, find a polyiamond that each can tile. |
 | Hexa-Penta-Tetriamonds. Given a hexiamond, a pentiamond, and a tetriamond, find a polyiamond that each can tile. |
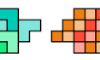 | Zucca's Challenge Problem for Extrominoes. Given a set of extended trominoes or trikings, find a polyking that each can tile and no others can tile. |
 | Zucca's Challenge Problem for Polyiamonds. Given a set of tetriamonds or pentiamonds, find a polyiamond that each can tile and no others of that order can tile. |
 | Zucca's Challenge Problem for Tetrahexes. Given a set of tetrahexes, find a polyhex that each can tile and no others can tile. |
 | Zucca's Challenge Problem for Polypents. Given a set of tripents or tetrapents, find a polypent that each can tile and no others of that order can tile. |